[Enunciado comum às Questões 3 e 4]
Uma força atua horizontalmente sobre um bloco de massa e que se encontra apoiado em uma parede vertical, como mostrado na figura. O coeficiente de atrito estático entre o bloco e a parede é . Considere o módulo da aceleração gravitacional no local .
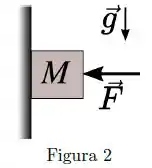
[Questão 3]
Considere as assertivas:
. Se , o bloco desce com aceleração constante.
. Se , o bloco permanece em repouso.
. Se , o bloco permanece em repouso.
Marque a alternativa abaixo contendo apenas as assertivas corretas.
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Passo 1
Temos um bloco sendo empurrado contra a parede.
Como a parede é vertical, sua tendência é deslizar para baixo devido à força Peso :
Entretanto, há uma força de atrito contra essa tendência, que possivelmente mantêm o bloco em quilíbrio.
Porque “possivelmente”?
Isso porque a força de atrito estático tem um valor máximo dado por:
Então, vamos analisar em cada afirmativa se a força de atrito é capaz de segurar o bloco ou não.
Passo 2
. Se , o bloco desce com aceleração constante.
. Se , o bloco permanece em repouso.
Vamos analisar essas duas juntas, porque ou o bloco vai cair com aceleração constante ou então ele vai permanecer em repouso.
Primeiro vamos fazer o Diagrama do Corpo Livre (D.C.L):
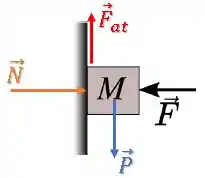
Vamos supor primeiro que o bloco está em equilíbrio...
No eixo , temos:
Como nas afirmativas e , temos que:
Já no eixo , temos:
Então, descobrimos que a força de atrito deve ter um valor igual a para que o bloco fique em equilíbrio.
Mas vamos olhar agora, o valor máximo que a força de atrito atinge.
Já vimos que ele será calculado com:
Substituindo os valores:
Então, a força de atrito necessária para segurar o bloco é maior que a força de atrito máxima.
Assim, como esse valor foi ultrapassado, o bloco entra em movimento e essa força de atrito passa a ser cinética, deixando o bloco descer com aceleração constante.
A afirmativa é verdadeira e a é falsa.
Passo 3
. Se , o bloco permanece em repouso.
Vamos fazer o mesmo procedimento e verificar se agora a força de atrito máxima é suficiente ou não para manter o bloco em equilíbrio.
O Diagrama do Corpo Livre será o mesmo:
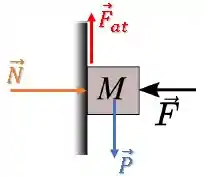
No eixo , temos:
Mas agora, a força vale :
Já no eixo , temos:
Essa é a força de atrito necessária para o bloco ficar em repouso.
Mas, a força de atrito máxima vai ser maior dessa vez, pois a normal aumentou:
Assim, a força de atrito máxima é maior que a força de atrito necessária para manter o equilíbrio, logo, o bloco não cai.
A afirmativa é verdadeira.
Como as afirmativas e são corretas, ficamos com a letra (e).
Resposta
Letra (e)