Na figura abaixo, as massas dos blocos 2 e 3 são e , respectivamente. O coeficiente de atrito cinético entre o bloco 2 e a mesa é 0,10 enquanto o coeficiente de atrito estático é 0,20. Despreze o atrito entre os blocos 1 e 2.
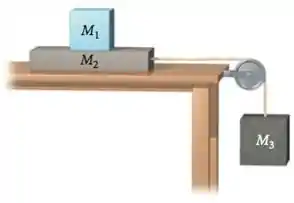
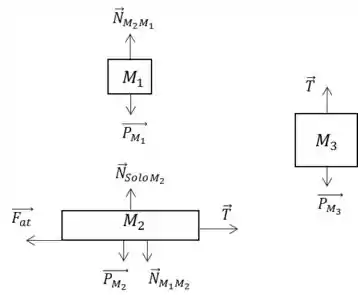
a) Usando a 3a Lei de Newton, faça o diagrama do corpo livre para cada um dos três blocos, indicando todos os pares de ação e reação.
b) Qual deve ser o valor mínimo da massa do bloco 1 para que o bloco 2 não se mova?
c) Calcule a aceleração do sistema se o bloco 1 é levantado.
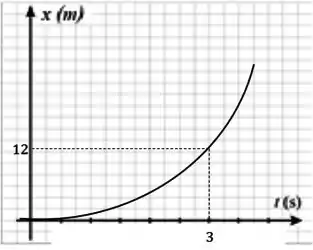
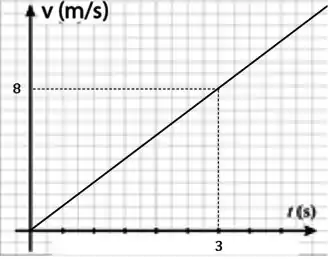
d) Esboce os gráficos da velocidade e da posição do bloco 2, desde o momento em que o bloco 1 é levantado até após este momento.
Passo 1
a)
As únicas forças de ação e reação do sistema são as forças de contato (forças Normais). São as forças e entre os blocos 1 e 2.
Passo 2
b)
Aplicando a segunda lei de Newton na direção do movimento. Podemos perceber que o bloco 1 não possui forças na horizontal, logo ele não se movimentará. Para os demais blocos ficará:
Bloco 2:
Bloco 3:
Se somarmos a equação do bloco 2 com a equação do bloco 3, teremos:
Ou seja, para o sistema não entrar em movimento, temos que ter:
Como estamos falando de um sistema estático, então essa força de atrito é a força de atrito estática máxima:
Como o bloco 2 está em equilíbrio na vertical, vamos ter:
O bloco 1 também está em equilíbrio na vertical, então vamos ter:
Como , podemos substituir na equação de equilíbrio vertical do bloco 2:
Agora sim! Finalmente chegamos onde queríamos, relacionar tudo isso com o peso do bloco 1. Agora vamos substituir na equação do movimento que fizemos lá atrás:
Substituindo os dados:
Passo 3
c)
Com o bloco 1 levantado vamos chegar a mesma equação do item anterior:
Substituindo a fórmula da força de atrito:
Só que como não temos mais o contato do bloco 1 com o bloco 2. Por conta, aplicando o equilíbrio na vertical para o bloco 2:
Substituindo:
Substituindo os dados:
Passo 4
d)
Se adotarmos a posição do bloco 2 como a origem, podemos calcular a velocidade e posição após .
Como a posição depende do tempo ao quadrado, essa função será representada como uma parábola.
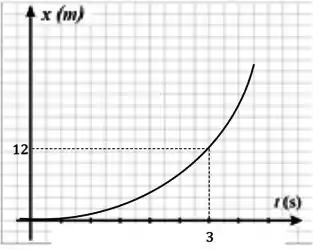
Agora calculando a velocidade em :
Como a velocidade depende linearmente do tempo, então essa função será representada por uma reta.
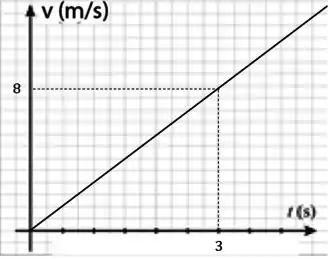
Resposta
a)
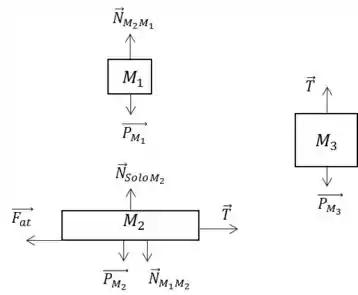
b)
c)
d)