Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Magnético Gerado por uma Bobina

Ver Teoria
Exercício 35123456789101112131415161718192021222324252627282930313233343637383940

Enunciado

Física 2 - UFF; P3 de 2019.1

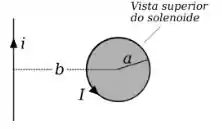
1 - A figura ao lado mostra um solenoide de raio a e densidade de espiras n transportando uma corrente I no sentido anti-horário (vista de cima). A uma distância b do centro do solenoide, um fio muito longo transporta uma corrente i . Quanto deve valer a corrente, i, que passa pelo fio para que o campo magnético no centro do solenoide seja nulo?

  1. i = I / 2 π b n
  2. i = I
  3. i = - I
  4. i = 2 π b n I a
  5. i = 0

Passo 1

Bem, pelo formulário, sabemos qual é o campo magnético de uma espira circular:

B e s p i r a = μ 0 i 2 d 2 + R 2 3 / 2

Só que esse campo é o campo referente ao eixo central da espira:

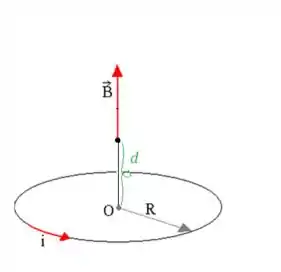
Onde d é a distância do centro da espira ao ponto de medição. Dessa forma, podemos concluir que o campo magnético no interior de uma espira de raio a será... (basta considerar d = 0 ):

B e s p i r a = μ 0 I a 2 2 a 2 3 2 =

B e s p i r a = μ 0 I a 2 2 a 3 =

μ 0 I 2 a

Porém, no nosso caso não temos uma espira, e sim n . Então, o campo magnético desse solenoide (conjunto de várias espiras) será:

B s o l e n o i d e = n μ 0 I 2 a

Agora, qual será a direção do campo? Bem, depende da regra da mão direita, certo? Aplicando a regra da mão direita no nosso problema...

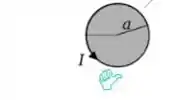
Podemos ver que o campo magnético do solenoide é então para cima (saindo da sua telinha e indicado pela bolinha vermelha):

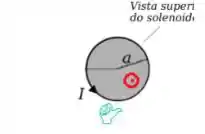
Passo 2

Junto a esse solenoide, temos um fio reto que passa a uma distância b do centro da espira e de corrente i :

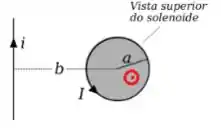
Esse fio também gera um campo elétrico no centro da bobina, e de intensidade dada pelo formulário...

B f i o = μ 0 i 2 π d

Onde d é à distância do fio ao ponto que queremos (centro do solenoide que está a uma distância d = b ):

B f i o = μ 0 i 2 π b

Esse campo, pela regra da mão direita, tem sentido contrário ao do solenoide (entrando na tela indicado pela bola roxa):

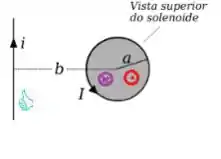
Passo 3

Então, devido às direções contrárias, podemos falar que no centro do solenoide o campo magnético total é igual ao campo do solenoide, menos o campo do fio:

B t o t a l = n μ 0 I 2 a - μ 0 i 2 π b

Para esse campo ser nulo, então...

n μ 0 I 2 a - μ 0 i 2 π b = 0     →

i 2 π b = n I 2 a       →

i = n I 2 π b a

Resposta

Letra D.

Exercícios de Livros Relacionados

79- Uma bobina de alto-falante. Na seção 27.7 , mostramos que era igual a zero a força resultante sobre uma espira de corrente em um campo magnético uniforme. A força magnética sobre uma bobina destin
87- Uso da Lei de Gauss do magnetismo. Em uma certa região do espaço, o campo magnético B → não é uniforme. O campo magnético possui um componente z e outro componente que aponta para fora ou para den
Um solenóide de comprimento 30 cm, raio 1,2 cm e 300 voltas, conduz corrente de 2,6 A. Determine a magnitude do campo magnético no eixo do solenóide:a) No centro do solenóide.b) Em uma extremidade do
Um solenóide tem n voltas por unidade de comprimento, raio R e conduz uma corrente I. Seu eixo coincide com o eixo z – uma extremidade em z = - 1 2 l e a outra em z = + 1 2 l . Mostre que a magnitude
Um único anel condutor tem raio igual a 3,0c m e conduz corrente igual a 2,6A . Qual é a magnitude do campo magnético na linha que passa pelo centro do anel e é perpendicular ao plano do anel a No cen