Exercícios de Campo Magnético Gerado por uma Bobina - Lista de Exercícios Resolvida

Qual é o módulo do momento dipolar magnético de um solenoide de 200 espiras, 25 cm de comprimento, 10 cm de diâmetro e corrente 0,29 A?

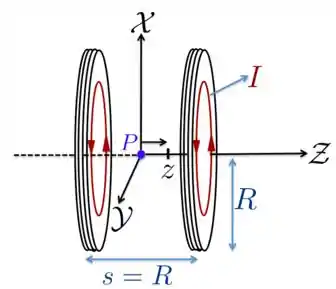
A figura abaixo mostra a seção reta de duas bobinas circulares com raio , cada uma delas com espiras que conduzem uma corrente no mesmo sentido. A distância entre as bobinas é igual ao raio das bobinas. As bobinas dessa configuração denominam-se bobinas de Helmholtz e produzem um campo magnético bastante uniforme na região entre elas. O ponto está à mesma distância do centro de cada uma das duas bobinas.

1. Deduza uma expressão para o módulo do campo magnétido em um ponto situado a uma distância à direita do ponto , que está no centro de simetria das bobinas.
2. Usando a expressão obtida no item a), obtenha o módulo do campo magnético exatamente sobre o ponto .
3. Calcule o valor do módulo do campo magnético no ponto , considerando espiras, e .

Uma bobina circular com espiras enroladas de modo compacto possui raio igual a e conduz uma corrente de . Quantas espiras ela deve ter para que o módulo do campo magnético seja de em um ponto sobre o eixo da bobina afastado de de seu centro?

Uma bobina circular com 600 espiras enroladas de modo compacto possui diâmetro igual a 4,0 cm e conduz uma corrente de 0,500 A. Qual é o módulo do campo magnético (a) no centro de bobina? (b) em um ponto sobre o eixo da bobina afastado 8,0 cm de seu centro.

Uma bobina circular de espiras enroladas de modo compacto possui raio de .

1. Qual deve ser a corrente que passa pela bobina, supondo que o campo magnético no centro da bobina é igual a ?
2. A que distância do centro da bobina, sobre o eixo da bobina, o campo magnético é igual à metade de seu valor no centro?

Uma bobina conduzindo uma corrente de é constituída por espiras circulares enroladas de modo compacto, cada uma com raio igual a .

1. Determine o módulo do campo magnético ao longo do eixo da bobina, situado a uma distância de do seu centro.
2. Em que ponto ao longo do eixo da bobina o campo magnético se reduz a do valor do campo no centro da bobina?
3. Determine o valor do momento de dipolo magnético que pode ser associado à essa bobina.

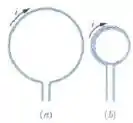
A figura abaixo mostra um fio que conduz uma corrente e forma uma bobina circular com apenas uma espira. Na figura um fio de mesmo comprimento forma uma bobina circular com duas espiras de raio igual à metade do raio da espira da figura .

Se e são os módulos dos campos magnéticos nos centros das duas bobinas, qual é o valor da razão ?

Qual é o valor da razão entre os momentos dipolares das duas bobinas?

A figura abaixo mostra um dispositivo conhecido como bobina de Helmholtz, formado por duas bobinas circulares coaxiais de raio , com espiras, separadas por uma distância . As duas bobinas conduzem correntes iguais no mesmo sentido. Determine o módulo do campo magnético no ponto , situado sobre o eixo das bobinas, a meio caminho entre elas.

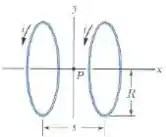
Dados:

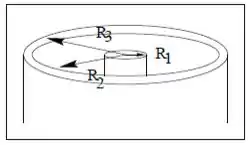
Uma bobina de espiras foi enrolada num corpo toroidal de raio interno , raio externo e altura , como indica a figura ao lado.

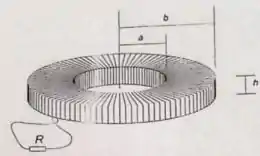
1. Os dois extremos do fio enrolado foram conectados com a ajuda de um resistor como mostra a figura. Desta maneira se formou um circuito . A resistência (incluindo a resistência do próprio fio) vale . Com a ajuda da lei de indução foi criada uma corrente neste circuito de tal maneira que em flui uma corrente de . A partir deste instante, o circuito foi deixado sem influência externa. Supondo que , e e calcule em quanto tempo a corrente no circuito diminui para o valor de . Dado: .

Uma bobina de espiras foi enrolada num corpo toroidal de raio interno , raio externo e altura , como indica a figura ao lado.

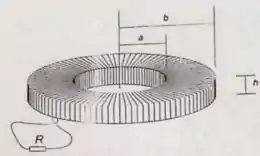
1. Escreva o campo magnético gerado por esta bobina quando flui uma corrente no fio enrolado.

Uma bobina de espiras foi enrolada num corpo toroidal de raio interno , raio externo e altura , como indica a figura ao lado.

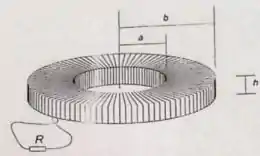
1. Calcule a autoindutância desta bobina usando o resultado do item a).

O campo magnético no centro de uma espira de diâmetro vale .

Qual a corrente da espira?

Um fio muito longo e reto conduz a mesma corrente que a espira do item . A que distância do fio o campo magnético é de ?

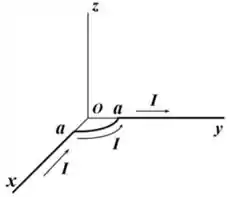
Uma corrente elétrica percorre um fio infinito que está alinhado com o eixo . Ao atingir a origem do sistema de coordenadas, o fio dá uma volta completa em torno do ponto .

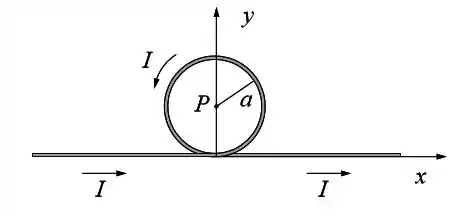
(a) Considerando apenas as partes retilíneas do fio, determine o vetor campo magnético no ponto .

(b) Calculo o vetor campo magnético produzido pelo trecho circular no ponto .

(c) Determine o vetor campo magnético total no ponto .

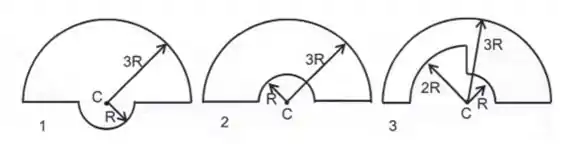
Os diagramas mostram três espiras que consistem em arcos circulares concêntricos (metade ou um quarto de círculos de raios , e ) e comprimentos radiais. Os circuitos conduzem a mesma corrente no mesmo sentido. Classificá-las de acordo com as magnitudes dos campos magnéticos que produzem em , de menor a maior.

(a)

(b)

(c)

(d)

(e)

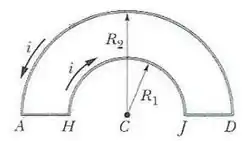
(A) Somente os trechos AH e JD contribuem para o vetor campo magnético total.

(B) Somente o trecho AD contribui para o vetor campo magnético total, pois o seu raio é maior.

(C) Somente o trecho HJ contribui para o vetor campo magnético total, pois o seu raio é menor.

(D) O vetor campo magnético total é perpendicular ao plano da página e aponta para dentro da página.

(E) O vetor campo magnético total é perpendicular ao plano da página e aponta para fora da página.

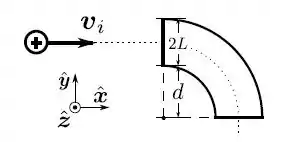
Um acelerador de partículas é projetado para desviar um próton, de massa e carga , que incida horizontalmente, com velocidade inicial , para uma velocidade final . Assinale o campo magnético constante que permite que isso aconteça.

Considere um toroide com espiras de raio interno e raio externo (ver figura). Cada espira é percorrida por uma corrente elétrica .

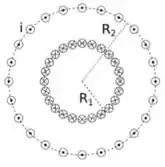
a) Determine o módulo do campo magnético no interior do toroide, i.e., para .

b) Se colocarmos no centro do toroide um fio longo e retilíneo, colinear com o eixo do toroide, qual é a intensidade e sentido da elétrica no fio que anulará o campo magnético no interior do toroide?

Esta questão é constituída de duas partes independentes.

Parte 1

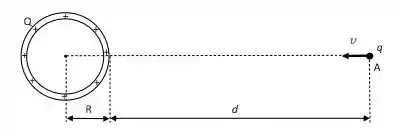
Uma casca esférica isolante de raio possui uma carga positiva uniformemente distribuída. Uma carga negativa e de massa passa pelo ponto A, a uma distância da superfície da casca, com velocidade em direção ao centro da casca esférica, como indicado na figura abaixo. A carga pode ser considerada tão pequena que não influencia a distribuição de cargas na casca esférica.

Nesta situação:

a) Calcule o potencial do ponto A.

b) Calcule a velocidade com a qual a carga irá colidir com a casca esférica.

Parte 2

Um sistema de placas planas e paralelas possui um diagrama de potencial de acordo com a figura abaixo.

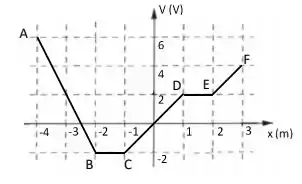
c) Faça o gráfico do valor do campo elétrico indicando claramente os valores do campo em cada região.

d) Na região entre os pontos D e E, a placa é isolante ou condutora? Justifique claramente a sua resposta.

e) Calcule a densidade superficial de carga na superfície B. (para os cálculos, considere )

Uma carga pontual positiva, , dada em está situada no centro de uma casca esférica condutora, em equilíbrio eletrostático e eletricamente neutra, de raio interno e raio externo , (), medidos em (veja figura abaixo).

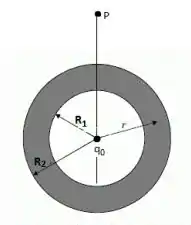
1. Quais as cargas induzidas, respectivamente, na superfície interna e na superfície externa da casca?
2. Seja a distância radial ao centro da casca esférica medida em . Calcule o vetor campo elétrico em todas as regiões do espaço, i.e., para , para , e para .

Q – Um circuito é formado por dois trechos retilíneos semi-infinitos e por um trecho semi-circular de raio , conforme mostrado na figura.

Nenhuma das alternativas

.

.  

.

.

Considere uma espira circular, localizada no plano , centrada na origem, transportando uma corrente estacionária , como mostrado na figura abaixo.

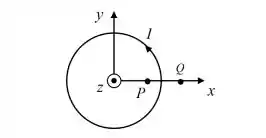
Qual é o sentido do campo magnético produzido pela espira nos pontos e , respectivamente, localizados sobre o eixo .

(a)

(b)

(c)

(d)

(e)

(f)

Considere o sistema, mostrado em corte na figura ao lado, que é constituído por uma casca cilíndrica fina de raio e comprimento infinito na qual flui uma corrente para cima e, coaxial a ela, uma outra casca cilíndrica, desta vez com raio interno e externo e também comprimento infinito, com uma corrente () apontando para baixo.

Calcule o vetor campo magnético em todas as regiões sabendo que as correntes estão distribuídas uniformemente.

Uma espira de comprimento , transportando uma corrente , pode ser enrolada na forma de uma circunferência uma vez (situação ) ou duas vezes (situação ). A razão entre as intensidades dos campos magnéticos no centro da espira nas situações e é dada por

A intensidade do campo magnético produzido no interior de um solenoide muito comprido percorrido por corrente elétrica, depende basicamente:

1. Do numero de espiras por unidade de comprimento e intensidade da corrente
2. Do diâmetro interno do solenoide
3. Só do numero de espiras do solenoide
4. Do comprimento do solenoide
5. Só da intensidade da corrente

Considere dois anéis circulares, um condutor e outro isolante, pertencentes a um mesmo plano, sujeitos a um campo magnético variável no tempo, perpendicular ao plano dos anéis.

Estando os dois anéis em repouso, em qual deles surgirá uma força eletromotriz induzida? Em qual deles surgirá uma corrente induzida?

Em nenhum dos anéis. Em nenhum dos anéis.

Em nenhum dos anéis. Somente no anel condutor.

Somente no anel condutor. Somente no anel condutor.

Em ambos os anéis. Somente no anel condutor.

Em ambos os anéis. Em ambos os anéis.

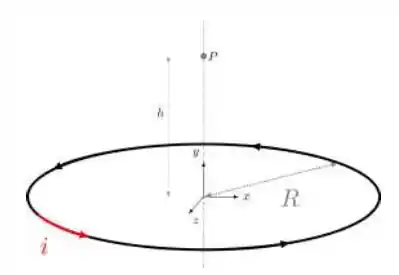
Considere uma espira circular de raio R no plano-xz com centro na origem do sistema de coordenadas, como mostra a figura. Essa espira é percorrida por uma corrente constante i no sentido anti-horário (também mostrado na figura).

a) Utilizando a Lei de Biot-Savart, encontre o valor do campo magnético total no ponto

mostrado na figura (o ponto se encontra no eixo-y).

b) Se introduzirmos nessa região do espaço um campo magnético externo constante:

calcule os vetores força magnética total e o torque na espira.

Um fio fino circular, de raio , é percorrido por uma corrente estacionária de intensidade . No mesmo plano, temos um outro fio, constituído por dois segmentos retilíneos, longos e um arco de semicircunferência, concêntrico com o primeiro fio, de raio , conforme mostra a figura.

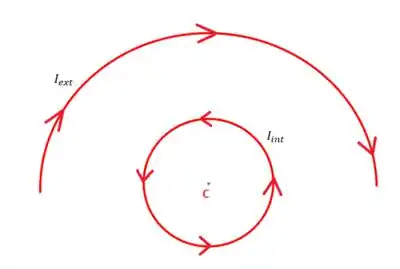
Qual deve ser a intensidade da corrente estacionária , nesse segundo fio, para que o campo magnético no centro comum seja nulo?

a)

b)

c)

d)

e)

Uma espira condutora e circular de raio , é percorrida por uma corrente elétrica de intensidade . Determine o valor do vetor indução magnética no centro da espira.

Dados: e

(Capítulo 29 – Problemas Adicionais – Exercício 90a) Na figura 29-71, um arranjo conhecido como bobina de Helmholtz é formado por duas bobinas coaxiais circulares de espiras e raio , separadas por uma distância . As duas bobinas conduzem uma corrente no mesmo sentido. (a) Mostre que a derivada primeira do módulo do campo magnético das bobinas, , é zero no ponto médio para qualquer valor de . Por que é razoável esperar que isso aconteça, tendo em vista a simetria da situação?

9 - Uma espira circular de raio transporta uma corrente constante. Marque o gráfico que melhor descreve a quantidade , onde B é o módulo do campo magnético produzido ao longo do eixo de simetria do sistema.

13 - Para que uma determinada engenhoca funcione corretamente é necessário que uma bobina de raio transportando uma corrente de seja imersa em um campo magnético constante . Contudo, também é necessário que o campo magnético no centro da bobina seja nulo. Para isso, precisamos garantir que:

1. O campo magnético produzido pela bobina esteja alinhado paralelamente ao campo magnético B e que a bobina possua espiras.
2. O campo magnético produzido pela bobina seja transversal ao campo magnético B e que a bobina possua espiras.
3. O campo magnético produzido pela bobina esteja alinhado antiparalelamente ao campo magnético B e que a bobina possua espiras.
4. O campo magnético produzido pela bobina esteja alinhado paralelamente ao campo magnético B e que a bobina possua espiras.
5. O campo magnético produzido pela bobina esteja alinhado antiparalelamente ao campo magnético B e que a bobina possua espiras.

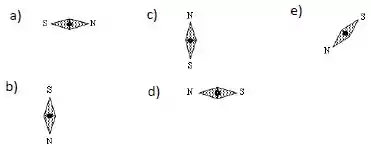
Duas espiras paralelas ao plano conduzem correntes no sentido anti-horário conforme indicado na figura.

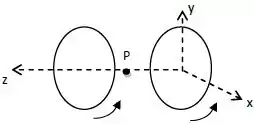
Os centros das espiras e o ponto , situado no ponto médio entre as espiras, estão sobre o eixo . Qual das figuras abaixo mostra a orientação de uma bússola quando colocada no ponto ?

A figura ilustra uma bobina com 1000 espiras circulares enroladas em um solenoide de comprimento e diâmetro . A corrente elétrica que circula na bobina produz um campo magnético de magnitude igual a próximo ao centro da bobina.

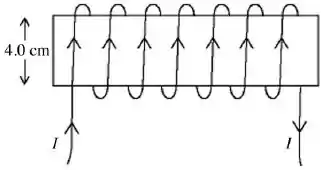
A intensidade da corrente vale:

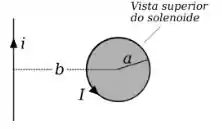
1 - A figura ao lado mostra um solenoide de raio e densidade de espiras transportando uma corrente no sentido anti-horário (vista de cima). A uma distância do centro do solenoide, um fio muito longo transporta uma corrente . Quanto deve valer a corrente, i, que passa pelo fio para que o campo magnético no centro do solenoide seja nulo?

4 - As linhas de campo magnético dentro do solenoide (atravessado pela corrente ) mostrado na figura abaixo são:

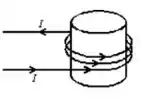
1. círculos concêntricos ao solenóide e orientados no sentido anti-horário, na mesma direção da corrente .
2. círculos concêntricos ao solenóide e orientados no sentido horário, na direção oposta a corrente .
3. paralelas ao eixo de simetria do solenóide e apontam para cima, em direção ao topo da página
4. paralelas ao eixo de simetria do solenóide e apontam para baixo, em direção ao pé da página.
5. indefinidas, desde que .

Um toroide de seção reta transversal circular uniformemente enrolado com voltas é preenchido com um material composto de oxigênio líquido, de constante de susceptibilidade magnética . O raio médio do toroide é de e o raio da seção transversal é . Se uma corrente de passa pelo fio, encontre qual foi o aumento do campo magnético devido à presença do oxigênio líquido.

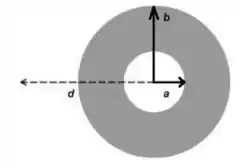
A figura abaixo mostra a seção reta de um cilindro com uma cavidade vazia de raio interno e raio externo . Uma densidade de corrente uniforme passa pelo cilindro. Com essas informações, qual é a intensidade do campo magnético em um ponto a uma distância do eixo do cilindro como destacado na figura?

A figura abaixo mostra uma Bobina de Helmholtz, um dispositivo utilizado para produzir uma região de campo magnético razoavelmente uniforme. Este dispositivo também é usado em aparatos de pesquisa para cancelar o campo magnético da Terra (entre diversas outras aplicações).

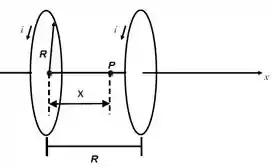
O dispositivo consiste de duas espiras circulares de raio , ambas perpendiculares ao eixo de simetria, com seus centros separados por uma distância também igual a . As duas carregam correntes fluindo no mesmo sentido.

1. Calcule o campo magnético sobre o eixo, devido à espira da esquerda, no ponto situado a uma distância (medida a partir do centro desta espira) entre as duas espiras (módulo, direção, sentido). ATENÇÃO: o ponto NÃO está situado no centro das espiras, mas em uma posição genérica do eixo entre as espiras.
2. Calcule o campo magnético no mesmo ponto devido à outra espira (módulo, direção, sentido).
3. Qual é o campo magnético total em (módulo, direção, sentido)?

Considere agora uma partícula carregada, , com carga negativa, que passa no ponto (onde o campo magnético é praticamente uniforme) com uma velocidade , onde é uma constante.

4. A partícula será defletida ou continuará na sua direção e sentido? Se mantiver direção e sentido, justifique. Se não, descreva qualitativamente em que direção e sentido a partícula será defletida.

Considere uma esfera isolante de raio com uma carga total distribuída de maneira esfericamente simétrica seguindo a densidade volumétrica de carga onde é a distância ao centro da esfera (Figura 1).

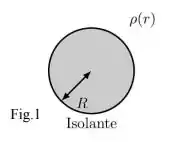
a) Encontre o campo elétrico na região externa à esfera

b) Encontre o valor de para que o campo elétrico no interior da esfera cresça com o quadrado da distância ; isto é, como . Para esse valor de , encontre .

Em seguida, a esfera é envolvida por uma casca esférica condutora de raio interno e raio externo, como mostra a Figura 2. Essa casca possui uma carga líquida desconhecida.

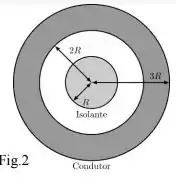
c) Encontre a densidade superficial de carga na parede interna da casca condutora (raio ).

d) Se o módulo do campo elétrico a uma distância for, qual é o valor da carga líquida ?