Os diagramas mostram três espiras que consistem em arcos circulares concêntricos (metade ou um quarto de círculos de raios , e ) e comprimentos radiais. Os circuitos conduzem a mesma corrente no mesmo sentido. Classificá-las de acordo com as magnitudes dos campos magnéticos que produzem em , de menor a maior.
(a)
(b)
(c)
(d)
(e)
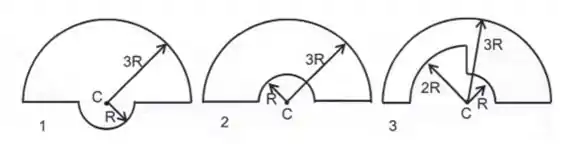
Passo 1
Aqui, vamos usar que o campo gerado pela espira é dado por:
Onde é a distância da espira para o ponto e é o comprimento do arco que estamos analisando.
Também é bom lembrarmos como fazemos para encontrar o comprimento de um arco:
Isso é, o comprimento do arco é igual ao raio multiplicado pelo ângulo do arco (em radianos!).
Passo 2
Para a figura , teremos dois comprimentos de arco que geram campo no ponto .
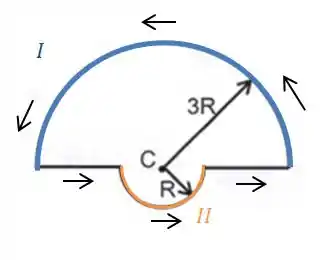
O campo gerado pelo arco será:
Onde será:
Portanto, temos:
O campo gerado pelo arco será:
Onde será:
Portanto, temos:
Olhando novamente para a figura, vemos que pela regra da mão direita, os campos gerados serão somados (no caso da figura, os dois campos estariam saindo do plano da página).
Por isso, o campo magnético total no ponto será a soma dos dois campos.
Passo 3
Para a figura , temos os seguintes arcos que geram campo:
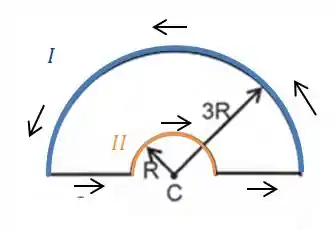
Que são os mesmos arcos da figura 1, e portanto os campos magnéticos gerados são o mesmo:
No entanto, se olharmos para a figura, vemos que pela regra da mão direita, o campo gerado pelos arcos no ponto são contrários (no caso da figura, o arco gera um campo para fora da página e o arco gera um campo para dentro da página).
Por conta disso, o campo magnético total no ponto será a subtração dos dois campos:
(Nessa ordem para obtermos um valor positivo, afinal, só queremos a magnitude do campo).
Passo 4
Para a figura , temos 3 arcos que geram campo magnético no ponto :
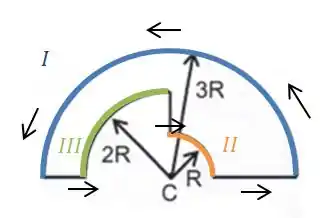
O arco é o mesmo arco dos casos anteriores e o seu campo vai ser:
O arco vai ter o campo dado por:
Onde o comprimento do arco será:
Portanto, teremos:
Finalmente, o arco vai ter o campo dado por:
Onde o comprimento do arco será:
Portanto, teremos:
Agora, precisamos voltar no desenho e verificar a direção desses campos.
Pela regra da mão direita, vemos que o campo gerado pelo arco é contrário aos gerados pelo arco e pelo . (No caso da figura, o campo gerado por sai do plano da página e os gerados por e entram no plano da página).
Por conta disso, o campo total será:
(Nessa ordem para obtermos um valor positivo.)
Passo 5
Classificando a magnitude dos campos, teremos:
Para sabermos a ordem, colocamos todos no mesmo denominador:
Colocando em ordem crescente, do menor para o maior, teremos:
Portanto,
Letra c)
Resposta
(c)