Dois pequenos discos, de massas e , se deslocam sobre uma mesa horizontal de coeficiente de atrito cinético com os discos . Inicialmente os discos possuem velocidades em direções perpendiculares cujos módulos são desconhecidos. Em um certo instante os discos colidem e passam a se deslocar juntos. Após a colisão o sistema se movimenta em uma direção que faz um ângulo com o eixo conforme a figura. Além disso observa-se que o sistema entra em repouso após percorrer uma distância desde o ponto onde ocorreu a colisão. Desprezando efeitos de rotação de cada disco, determine:
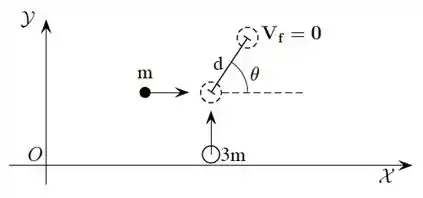
(b) Os vetores velocidade de cada disco no instante imediatamente anterior à colisão ocorrer.
(c) O vetor velocidade do centro de massa do sistema formado pelos discos no instante imediatamente anterior à colisão ocorrer.
Passo 1
(b) Conservação do momento linear
Geralmente em colisões temos que usar conservação do momento linear, sempre invocando que sobre o sistema não há força externa. Só que nesse problema temos o atrito que é, com certeza, uma força externa.
E agora? Como faz? Será que podemos usar a conservação de momento?????
A resposta é SIM!!! Mas tomando cuidado!
Somente nos momentos logo antes e logo depois da colisão podemos usar a conservação de momento! Isso por que nesse intervalo de tempo (que é muito pequenininho!) em que ocorre a colisão o atrito quase não atua de forma que podemos desconsiderá-lo!
Agora entre o ínicio e o fim do movimento dos discos não podemos usar a conservação de momento linear (até por que inicialmente os discos se movem e no final estão parados) por que o atrito já agiu o suficiente para não ser desconsiderado.
Já que é assim, podemos trabalhar com a conservação do momento linear!
É sempre bom tomar cuidado com o que a gente chama de inicial e final. Na nossa questão, vamos considerar como inicial o momento linear dos dois discos separadamente, beleza? E no final, dos dois discos juntos imediatamente após a colisão. Assim, nem no estado inicial nem no final iremos falar de atrito.
Passo 2
Teorema Trabalho-Energia Cinética
Depois da colisão, temos que considerar de fato o atrito atuando!
Tá, mas e daí? Lembra do Teorema Trabalho-Energia Cinética? Se não lembra, dá uma olhada:
Podemos relacionar o trabalho da força de atrito com a velocidade do sistema de discos após a colisão através desse teorema. Como no final do movimento, os dois discos colados param, do teorema a gente consegue tirar:
Passo 3
Considerar direção e sentido das velocidades

No passo anterior a gente encontrou a velocidade dos dois discos unidos não é mesmo? Pra gente conseguir achar a velocidade dos discos antes da colisão, vamos ter que analisar as componentes dos vetores de velocidade. Mas calma, não se desespere, vamos dar uma olhada na velocidade que já encontramos, pois podemos reescrever ela da seguinte forma:
E isso nos ajuda em alguma coisa? Parece que não mas se olharmos o resultado do Passo 1, vai ficar tudo mais claro:
E assim, temos:
Passo 4
(c) Pela Teorema Trabalho-Energia Cinética no item , achamos o módulo da velocidade do sistema com dois discos, lembra? Como o momento linear desse sistema de discos está posicionado no centro de massa, temos:
Mas isso é somente o módulo da velocidade! Na forma vetorial, escrevemos
Resposta
b)
c)