Considere um potencial, descrevendo uma força conservativa, dado pela função:
- Faça o gráfico da função potencial e da força associada a este potencial, indicando os pontos de máximo e mínimos locais, os pontos que e , e os valores assintóticos para os limites de e
- Desejamos empregar este potencial para aprisionar uma partícula de massa M. Qual é a velocidade máxima da partícula, em x = 0, para que a mesma fique confinada no potencial?
- Para uma partícula com velocidade , vinda de A, podemos realizar o aprisionamento adicionando uma força dissipativa: na região entre , a partícula sofre pequenas variações de momento , opostas ao seu deslocamento, a um intervalo médio (muito menor que o tempo de voo nesta região), resultando em uma força de atrito constante se sua velocidade não for nula. Qual a velocidade máxima de aprisionamento da partícula em função dos parâmetros desta armadilha?
Passo 1
-
Questãozinha meio “Cálculo 1”, mas vamos lá! Haha
No gráfico do potencial teremos uma parábola de concavidade voltada para cima entre os valores de e uma curva que decresce em para valores maiores que e menores que
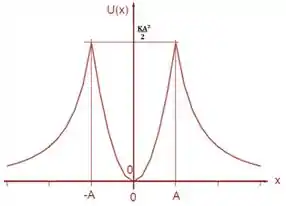
Passo 2
Já para a força, sabemos que pode ser calculada por:
Para o intervalo entre –A e A, teremos que:
Já para valores menor que –A e maior que A, a gente vai ter:
Isso nos dará o seguinte gráfico:
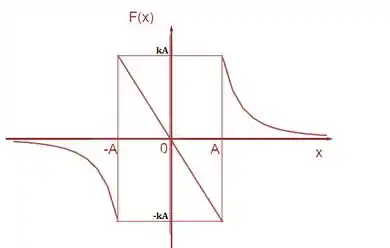
Tanto no gráfico de quanto o do eles tocam o eixo x e . Só existe mínimo local no gráfico do potencial, situado na origem do sistema.
Nos limites assintóticos ambas as funções tendem a zero.
Passo 3
b)
Em a gente viu que temos um mínimo de potencial, ou seja, teremos uma energia cinética máxima. Desta forma, devemos achar o ponto em que o potencial seja máximo, para considerar que a energia cinética seja mínima.
Pela conservação da energia mecânica, teremos:
Pela gráfico a gente vê que
Assim, podemos reescrever...
Para uma partícula ficar confinada temos que ter . Assim, teremos que:
Passo 4
c)
Vamos pensar da seguinte forma:
Se não houvesse atrito, como a velocidade seria , sendo a partícula iria embora e não ficaria aprisionada! :X
Mas daí, como o enunciado nos afirma que existe atrito e esse atrito vai frear nossa partícula até deixá-la com velocidade pequena o suficiente para deixá-la presa!
Assim, podemos escrever que a energia cinética terá que ser dissipada pelo trabalho da força de atrito para ficar dentro do potencial . Em outras palavras...
Desenvolvendo melhor isso aqui, teremos:
Mas e quem seria esse
Simples! Como nossa força de atrito é constante, podemos calcular o trabalho como
Mas como , teremos que:
Passo 5
Mas e quem seria esse
Simples! Como nossa força de atrito é constante, podemos calcular o trabalho como
Mas como , teremos que:
Plim! Temos nossa resposta!
Para ficar aprisionada nessa situação uma partícula deve ter velocidade , ou seja...
Resposta
Resposta
Ei, a resposta está no passo a passo :)