A energia potencial de um sistema é dada pela função .
a) Determine a força como uma função de ;
b) Para quais valores de a força é nula?
c) Faça o gráfico de versus ;
d) Faça o gráfico de versus e indique os pontos de equilíbrio estável e instável.
Passo 1
a)
Lembrando a fórmula:
Basta substituir a equação de e derivar, não esquecendo do sinal negativo na frente da derivada. Vamos lá, então:
Passo 2
b)
Já possuímos a equação de em função de , basta igualar a zero e encontrar os valores de que satisfazem a equação.
Resolvendo as raízes da equação utilizando Bhaskará:
Passo 3
c)
Para fazer o gráfico de por basta fazer o gráfico da função que a gente achou para , ou seja, o gráfico de:
Que é uma equação do segundo grau, de concavidade virada pra cima e com raízes e . Logo, teremos:
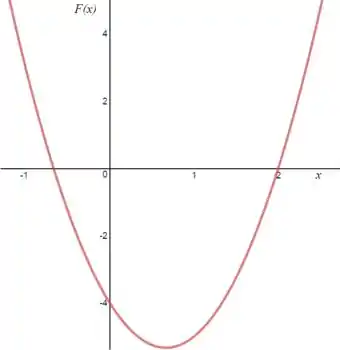
Passo 4
d)
É! Aqui vamos ter que plotar a equação do 3° grau. Essa função não é tãão comum de nos pedirem para desenhar, mas é importante saber desenha-la.
Precisamos de pelo menos três pontos para que a gente possa ter um feeling de onde se posicionam os extremos da função. Sabemos que um máximo local é em , um mínimo local é , que ela não possui mais nenhum lugar onde a inclinação é nula, e que ele passa no ponto (0,0). Assim, podemos deduzir que a função é mais ou menos essa aqui:
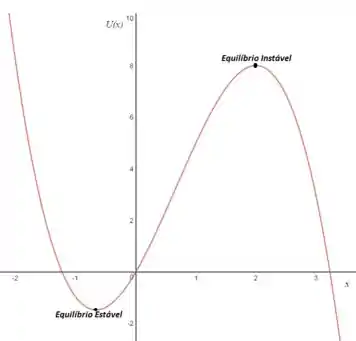
Já te dei o spoiler de onde são os pontos de equilíbrio estável e instável, mas já sabemos que existe equilíbrio onde a força é nula, certo? Ou seja, nos pontos que encontramos na letra b. Pensando como se fosse uma bolinha correndo no gráfico, se eu colocar uma bolinha em e der um empurrãozinho pra qualquer um dos lados ela não voltará, certo? Logo ali temos um equilíbrio instável.
Já para se eu der um mini empurrão a bolinha tenderá a voltar pra , né? Então aí é o ponto de equilíbrio estável!! :D~
Resposta
Indicadas! :DDDDDDDDD