Uma partícula se movimenta em uma dimensão sob a influência de uma força resultante conservativa, cuja energia potencial está mostrada na figura.
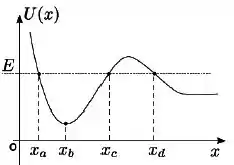
Sabendo que a energia mecânica da partícula é e que inicialmente ela se encontra na posição , é correto afirmar que:
(a) Ela nunca passa pela posição .
(b) é um ponto de equilíbrio estável pois nele a força resultante sobre a partícula é nula.
(c) é um ponto de retorno pois nele a energia cinética é nula.
(d) A energia cinética da partícula é mínima em .
(e) é um ponto de equilíbrio instável pois nele a energia cinética é nula.
(f) A energia cinética da partícula é máxima em .
Passo 1
O enunciado diz que a única força atuando sobre a partícula é uma força conservativa.
Ou seja, a força não retira nenhuma energia do sistema. O que ela faz é converter energia cinética em energia potencial e vice-versa, de forma que a soma delas duas seja sempre constante:
Po, beleza.
Mas o que acontece quando a energia potencial atinge o mesmo valor da energia total ?
Bom, quando isso acontece, toda a energia está na forma de potencial e não sobra nenhuma parcela na forma de energia cinética.
Portanto, nesses dois pontos e , a velocidade da partícula chega a zero e ela retorna na outra direção. Esses são chamados os pontos de retorno e eles estão delimitando o movimento da partícula, pois ela nunca terá energia suficiente para ultrapassá-los.
Vamos analisar as opções.
Passo 2
(a) Ela nunca passa pela posição .
Como vimos no Passo 1, os pontos de retorno e delimitam o movimento, portanto, a partícula nunca passa pela posição já que esse ponto está fora desse limite.
Ficamos com a resposta da letra (a), mas vamos dar uma olhada nas outras.
Passo 3
(b) é um ponto de equilíbrio estável pois nele a força resultante sobre a partícula é nula.
Isso está incorreto.
O ponto é um ponto de retorno, logo a velocidade da partícula nesse ponto é nula.
Já a força, é dada por menos a derivada do gráfico de energia potencial:
Então, como o gráfico tem uma certa inclinação nesse ponto, sua derivada não é nula e por isso a força não é nula.
Passo 4
(c) é um ponto de retorno pois nele a energia cinética é nula.
(d) A energia cinética da partícula é mínima em .
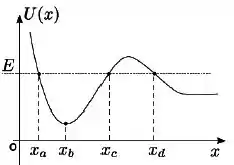
Vimos que os pontos de retorno são e , onde a energia potencial apresenta o mesmo valor da energia total.
No ponto em contrapartida, isso não acontece, inclusive, ele é o ponto de energia potancial mínima, o que significa que a energia cinética é máxima.
As afirmativa (c) e (d) são falsas.
Passo 5
(e) é um ponto de equilíbrio instável pois nele a energia cinética é nula.
(f) A energia cinética da partícula é máxima em .
A parte da letra (e) que diz que a energia cinética é nula no ponto está correta.
A energia cinética realmente é nula, mas isso não faz parte da definição de um equilíbrio instável.
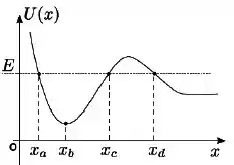
Temos um caso de um equilíbrio estável aqui, pois a partícula fica sempre oscilando entre os pontos e , ou seja, a força conservativa sempre atrai a partícula de volta uma vez que ela chega no limite do movimento.
Diferentemente de um equilíbrio instável, onde a partícula não retorna.
Ambas afirmativas são falsas.
Resposta
Letra (a)