Uma partícula de massa executa um movimento unidimensional e possui energia potencial cuja dependência com a coordenada é onde a e b são constantes positivas.
(a) Encontre a expressão da força que atua sobre a partícula como função da posição;
(b) Faça esboços das funções energia potencial e força como funções da posição da partícula.
(c) Encontre a(s) posição(ões) de equilíbrio da partícula sob a ação dessa força e classifique-o(s) de acordo com a estabilidade;
(d) Determine qual(ais) o(s) intervalo(s) de energia mecânica para o(s) qual(is) uma partícula sujeita a essa força possui movimento numa região limitada da reta.
(e) Determine qual(ais) o(s) intervalo(s) de energia mecânica para o(s) qual(is) uma partícula sujeita a essa força pode ser encontrada a distâncias arbitrariamente grandes da origem.
Passo 1
(a)
Basta lembrar que da fórmula que diz que a força é igual a menos a derivada da energia potencial, logo:
Passo 2
(b)
Esboços de e
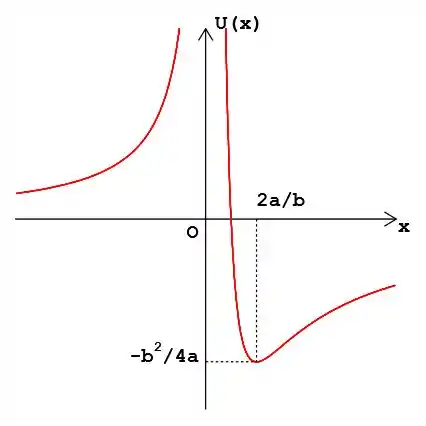
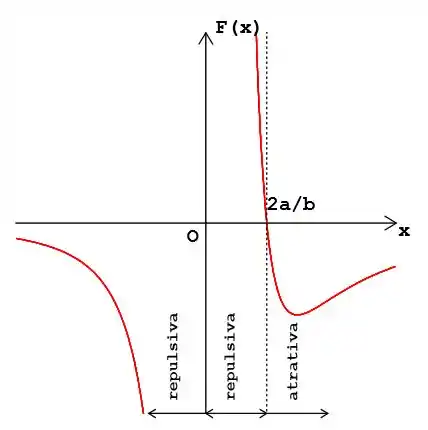
Passo 3
(c)
As posições de equilíbrio correspondem a pontos da reta em que a força é nula, ou seja, nesse caso, há um único ponto que satisfaz essa condição:
A estabilidade pode ser determinada por meio do sinal da segunda derivada de no ponto de equilíbrio:
Ou seja, a concavidade é voltada para cima, e portanto temos um ponto de equilíbrio estável.
Passo 4
(d)
Para valores de energia mecânica total no intervalo:
Uma partícula posta na região está confinada a mover-se entre os pontos e dados por:
Logo:
Passo 5
(e)
Na região , no caso de energia mecânica positiva , a partícula não pode ser encontrada a distâncias menores do que , mas pode se afastar da origem por distâncias arbitrariamente grandes, movendo-se no sentido de positivo. Na região , a energia mecânica mínima é zero e a partícula não pode ser encontrada a distâncias menores do que , mas pode se afastar da origem por distâncias arbitrariamente grandes, movendo-se no sentido de negativo.
Resposta
Resposta