Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Inequações produto-quociente

Ver Teoria
Exercício 16123456789101112131415171819202122232425262728293031323334353637383940414243444546

Enunciado

UFF, Cálculo IA-Lista 1, GMA, 2008-1, 5

Resolva a inequação:

2 x - 1 1 - x < 0

Passo 1

Essa inequação possui dois termos com x que se dividem. Vamos analisar o sinal de cada termo separadamente pra depois aplicar o quadrinho dos sinais.

2 x - 1 = 0 → x = 1 2

2 x - 1   é   n e g a t i v o   q u a n d o :   x < 1 2

2 x - 1   é   p o s i t i v o   q u a n d o :   x > 1 2

1 - x = 0 → x = 1

1 - x   é   n e g a t i v o   q u a n d o :   x > 1

1 - x   é   p o s i t i v o   q u a n d o :   x < 1

Passo 2

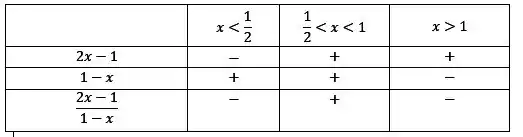Agora vamos fazer o quadrinho dos sinais, já que os dois termos formam um quociente.

Então, a resposta é

2 x - 1 1 - x < 0

quando

x < 1 2   o u   x > 1

Resposta

x < 1 2   o u   x > 1

Exercícios de Livros Relacionados

Demonstrar:Se 0ab , então sqrt(a b)(a + b)/(2) .
Use um gráfico para encontrar um número δ tal que se 5x5 + δ ent��o x ² x - 5100 ²