Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.
(a) Se T : R² → R² é uma transformação linear tal que é base ortonormal de R² , então T é ortogonalmente diagonalizável.
(b) Se u, v e w são vetores não nulos e tais que , então .
(c) Se u, v e w são vetores não nulos de R³ e tais que , então
(d) Se u e v são vetores do R³ ortogonais e de mesmo módulo, então
(e) Se u e v são vetores não nulos e com a mesma direção, então
Passo 1
Para iniciar essa ideia, vamos pensar na seguinte transformação:
Se pensarmos na seguinte transformação:
Essa vai ser a base ortonormal do , pois os se fizermos o produto interno teremos:
Além disso o módulo dos dois vetores é 1.
Vamos verificar se ele é diagonalizável, para isso primeiro acharemos os autovalores, para isso teremos:
Mas essa equação não tem solução real, então T não é diagonalizável!
T não é diagonalizável, logo também não será ortogonalmente diagonalizável.
Portanto, FALSA.
Passo 2
Vamos a letra b, precisamos pensar em um contra exemplo ...
Vamos supor vetores para u, v e w. Pegaremos os seguintes vetores:
Para esses valores essa afirmativa será falsa, observe só:
MAAAAAAS, vemos claramente que
Então, nossa segunda afirmativa é FALSA!
Passo 3
Essa letra c é muito parecida com a b...
Vamos novamente pensar num contraexemplo, tomemos por exemplo:
Para esses valores essa afirmativa será falsa, observe só:
Porém, no entanto, todavia....
Vemos claramente que !!
Então, nossa terceira afirmativa é FALSA!
Passo 4
Partiu letra d agora, estamos quase acabando ...
Vamos pensar no que diz o enunciado, se temos os vetores u e v ortogonais e com o mesmo módulo, o paralelogramo formado por esses dois vetores, tem uma área:
No entanto, sabemos que a área do mesmo é dada pelo módulo de , que acabamos de ver que é igual a .
Portanto, a nossa afirmativa é VERDADEIRA!!
Passo 5
Vamos para nossa última letra!
Observe os vetores na figura abaixo...
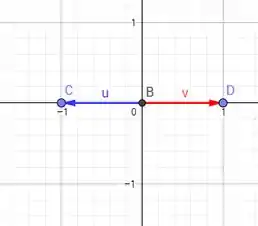
Concorda comigo que eles têm a mesma direção?
Estamos dizendo que
Se fizermos , teremos:
Ora ora, se fizermos o módulo de , vemos que o tamanho presente no gráfico corresponde a 2, ou seja:
OU SEJAAAA...
FALSO, MUITO FALSO! Rs
Resposta
a)FALSO
b)FALSO
c)FALSO
d)VERDADEIRO
e)FALSO