Exercícios de Produto Misto - Lista de Exercícios Resolvida

Calcule sendo .

Demonstre que geometricamente o produto misto é igual em módulo ao volume do paralelepípedo determinado pelos vetores e .

Verificar se são coplanares os seguintes vetores:

Encontre o volume do paralelepípedo determinado pelos vetores nos seguintes casos:

1. Dados os pontos tome .

Para que valor de os pontos são coplanares?

Verificar se os pontos estão no mesmo plano.

Sejam os vetores

Determinar o volume do paralelepípedo definido por .

Calcular o volume do tetraedro cujos vértices são:

Qual deve ser o valor de para que os vetores sejam coplanares?

Dados os vetores , calcular os valores possíveis de para que o volume do paralelepípedo determinado por seja 24 unidades de volume.

Considere fixada uma orientação em . Sejam três vetores mutuamente ortogonais de norma 1. Considere as seguintes afirmações:

1. é uma base positiva se

2. Apenas uma das bases e é positiva

3. O volume do paralelepípedo definido pelos vetores é igual a

Então

a) Apenas 1 e 2 são verdadeiras

b) Apenas 3 é verdadeira

c) 1, 2 e 3 são verdadeiras

d) Apenas 2 é verdadeira

e) Apenas 1 é verdadeira

f) 1, 2 e 3 são falsas

g) Apenas 2 e 3 são verdadeiras

h) Apenas 1 e 3 são verdadeiras

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.

(d) Se e são vetores de não nulos e ortogonais entre si, então .

(e) Se e são vetores de não nulos e ortogonais entre si, então

O volume do tetraedro de vértices , em que , e , é igual a

a)

b)

c)

d)

e)

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.

(a) Se T : R² → R² é uma transformação linear tal que é base ortonormal de R² , então T é ortogonalmente diagonalizável.

(b) Se u, v e w são vetores não nulos e tais que , então .

(c) Se u, v e w são vetores não nulos de R³ e tais que , então

(d) Se u e v são vetores do R³ ortogonais e de mesmo módulo, então

(e) Se u e v são vetores não nulos e com a mesma direção, então

Considere os pontos

e os vetores:

(a) Determine se existe um plano que contém os pontos A, B, C e D.

Em , as retas e determinam, com o plano , um tetraedro T. Então, a altura de T em relação à face contida em vale

Seja uma base ortonormal e, nesta base, considere os vetores , , e . Determine o vetor sabendo que e .

Sabendo-se que ABCD é um tetraedro de volume 36 e que os pontos M, N são tais que e , pode-se concluir que o volume do tetraedro ABMN é igual a:

Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.

A altura do tetraedro de vértices relativa à face é

a)

b)

c)

d)

e)

f)

Sabendo que . Calcule .

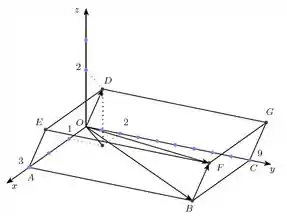
Considere o paralelepípedo oblíquo representado abaixo no sistema de coordenadas tridimensional.

a) Determine as coordenadas do ponto .

b) Calcule o volume do paralelepípedo.

Considere três vetores , e tais que . Calcule .

Em uma base ortonormal são dados os vetores , e .

1. Mostre que , , e são vértices de um tetraedro.
2. Calcule a área de face .
3. Calcule o volume desse tetraedro.

Sejam os vértices de um tetraedro cuja base é um triângulo de área igual a e cuja altura em relação a essa base tem comprimento igual a . Se

Então o volume do paralelepípedo determinado pelos vetores e é igual a

a)

b)

c)

d)

e)