Duas pequenas esferas carregadas, cada uma de massa , estão suspensas por fios de comprimento , conforme diagrama abaixo. Um campo elétrico uniforme e aplicado ao longo da direção . As esferas possuem cargas iguais a e .
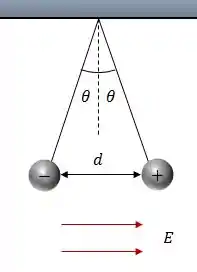
Determine:
A força elétrica em função de e , sobre cada esfera de modo que o conjunto fique em equilíbrio;
O campo elétrico nas mesmas condições dadas no item ;
A tensão no fio nas mesmas condições dadas no item ;
Passo 1
A força elétrica em função de e , sobre cada esfera de modo que o conjunto fique em equilíbrio;
Antes de começar, vamos entender mais ou menos o que acontece nesse problema.
Temos duas esferas de cargas e que irão gerar uma força elétrica de atração entre si, vamos chamar essa força de .
Além disso, essas cargas estão sobre a presença de um campo elétrico que também irá gerar uma força elétrica nas cargas, vamos chamar essa força de .
Ambas as forças são forças elétricas e, por conta disso, vamos soma-las e chama-la de .
Agora, para encontrar o valor da força elétrica que mantêm as cargas em equilíbrio, precisamos fazer o diagrama do corpo livre:
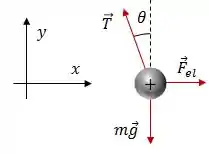
Como o sistema está em equilíbrio, podemos dizer que:
A partir da segunda equação, podemos escrever:
Substituindo isso na primeira equação, teremos:
Passo 2
O campo elétrico nas mesmas condições dadas no item ;
Como vimos no Passo 1, a força elétrica será pela interação entre as cargas e pela interação com o campo elétrico :
A gente sabe que a força gerada por um campo uniforme tem módulo dada por:
A força de interação tem módulo
Onde é a distância entre as bolinhas.
De acordo com a geometria do problema, podemos dizer que:
Logo,
Passo 3
Agora precisamos definir o sentido dessas forças. Para isso a gente tem que lembrar que como as cargas das bolinhas são contrárias, a força de interação tende a atraí-las. Para a força do campo a gente tem que lembrar que se a carga for positiva a força tem o mesmo sentido do campo, caso contrário será o sentido oposto ao campo.
Então no nosso problema vamos ter isso aqui:
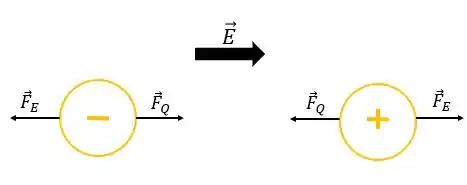
Ou seja, independente da bolinha que a gente considere, uma força é oposta a outra! Vou considerar o sentido positivo para a direita e analisar a bolinha positiva. Teremos então:
Finalmente:
Agora precisamos somente substituir a expressão da força elétrica que calculamos no item :
Passo 4
Pra terminar com isso, só falta isolar o e arrumar a bagunça:
Finalmente:
Passo 5
A tensão no fio nas mesmas condições dadas no item .
Podemos escrever a seguinte expressão para a tensão, obtida anteriormente:
Resposta