Duas pequenas esferas carregadas, cada uma de massa igual a , estão suspensas por fios de comprimento , conforme o diagrama abaixo.
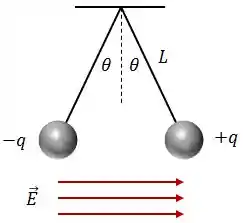
Um campo elétrico uniforme é aplicado ao longo da direção . As esferas possuem cargas elétricas e , como na figura ao lado.
Determine:
- O vetor força elétrica total, em termos de , , e do ângulo , sobre cada uma das esferas de modo que o conjunto fique em equilíbrio;
- O campo elétrico total sobre a carga positiva devido ao campo e à carga negativa, quando o sistema está em equilíbrio;
- A tração no fio;
Passo 1
- O vetor força elétrica total, em termos de , , , e do ângulo , sobre cada uma das esferas de modo que o conjunto fique em equilíbrio;
Beleza! Vamos nessa!
Cada carga aqui está sofrendo a ação de duas forças elétricas: a força que uma carga faz sobre a outra e a força que o campo elétrico faz sobre elas, certo?
A gente já sabe que cargas iguais se repelem e cargas opostas se atraem. Essa força de repulsão ou de atração é dada por:
Além disso, a força exercida sobre uma carga por um campo elétrico é dada por:
Passo 2
Já que as cargas aqui são opostas, sabemos que elas estão se atraindo, e a força elétrica entre elas será:
Onde é a distância entre as cargas. Olhando direito pra esse triângulo... dá pra relacionar , e com uma relação de seno, conseguiu enxergar? É como se dividíssemos esse triângulo em dois triângulos retângulos.
Assim, podemos dizer que:
Logo:
O sinal negativo aparece pra mostrar que as cargas estão se atraindo.
Obs: Como já temos ideia do vetor de força de atração entre as cargas, trabalhamos só com o módulo aqui, a gente discute sobre o vetor daqui a pouco.
A força gerada pelo campo elétrico aqui vai depender de qual carga estamos falando... sobre a carga negativa, a força será:
E sobre a carga positiva, a força será:
Beleza, agora vamos analisar esses vetores pra cada uma das cargas.
Passo 3
- Carga positiva:
- Carga negativa:
Sobrea carga positiva, a força de atração vai estar apontando na direção da carga negativa (sentido ) e a força gerada pelo campo elétrico, sobre a carga positiva, vai apontar no mesmo sentido do campo, logo:
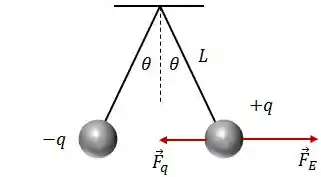
Ah! Eu chamei de a força de atração entre as cargas e a força gerada pelo campo elétrico, só pra diferenciar. Então, a força elétrica resultante será:
Sobrea carga negativa, a força de atração vai estar apontando na direção da carga positiva (sentido ) e a força gerada pelo campo elétrico, sobre a carga negativa, vai apontar no sentido contrário ao do campo, logo:
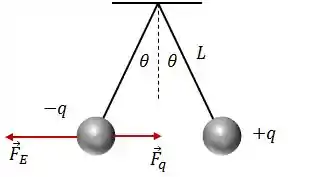
A força elétrica resultante será:
Passo 2
Então, aqui não tem mistério.
Você pode até pegar e escrever o campo elétrico gerado pela interação entre as cargas, ver o sentido desse campo elétrico e tal... ou você pode fazer do jeito mais fácil.
Já vimos que a força elétrica total sobre a carga positiva é dada por:
Por definição, podemos associar essa força elétrica total com o campo elétrico total através da relação:
Logo:
Passo 3
Ok, vou começar pela carga positiva. Pra calcularmos a tração no fio, primeiro precisamos desenhar todas as forças que estão agindo sobre a carga. Como o problema fala que a carga tem massa , teremos que levar em consideração também o peso da carga.
Assim, sobre a carga positiva, teremos:
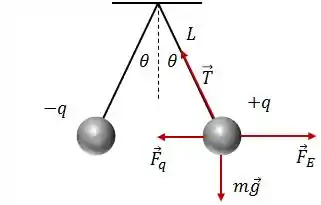
O que temos que fazer aqui é encontrar as componentes dessas forças na direção da força de tração do fio. Pra isso, vamos usar ângulo ali. Pra simplificar, vamos fazer o diagrama de corpo livre dessa carga positiva:
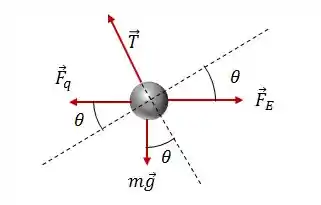
Escrevendo as forças na direção da tração, teremos:
Como o problema é simétrico, se calcularmos para a carga negativa, vamos encontrar o mesmo valor para tração.
Resposta
a.
b.
c.