Resolva utilizando Transformada de Laplace
Sendo a função dada por
Passo 1
Antes de tudo, precisamos escrever como função degrau, vamos fazer um esboço dela para entender melhor o que está acontecendo.
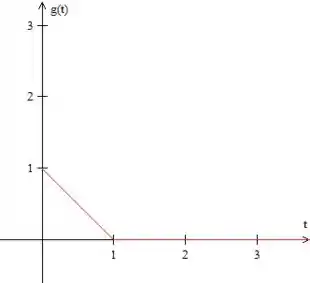
Isso é o mesmo que o seguinte:
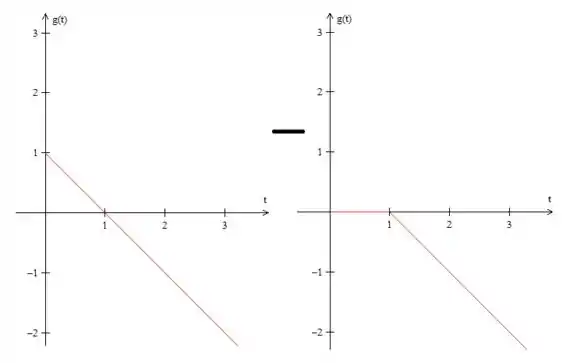
O 1º gráfico representa a função e o 2º representa essa função porém apenas a partir de , ou seja, (antes de a função vale zero e depois vale ) . Podemos escrever então:
Passo 2
Vamos aplicar a Transformada de Laplace à equação.Temos o seguinte:
Aplicando a fórmula
Temos
Precisamos de então
Agora vamos aplicar aquela propriedade da Transformada da derivada:
Substituindo na equação, temos:
Passo 3
Vamos, então, substituir os valores iniciais e isolar . Temos e .
Não vamos juntar essas frações para facilitar nossa vida nas frações parciais, ok?
Passo 4
Certo, agora temos que decompor essas frações em frações parciais, não é? Se você reparar, o denominador das duas últimas frações não pode ser fatorado, então vamos deixar elas de lado por enquanto! Agora vamos nos preocupar só com essas duas:
E seguir o mesmo passo a passo de sempre.
- Fatorar os denominadores
- Igualar a fração à soma de frações com denominadores iguais aos termos que encontramos.
- Fazer o MMC dessas frações, juntá-las ao mesmo denominador.
- Agora, partindo do princípio que essas duas frações são iguais, vamos encontrar os coeficientes das frações parciais.
- Agora que já temos os coeficientes basta reescrever as frações que criamos.
Bom, eles já estão fatorados, não temos muito o que fazer!
Aqui temos um detalhezinho: sempre que você encontrar termos iguais no denominador , um fator elevado ao quadrado, ao cubo, etc, você tem que fazer frações desse tipo:
Ou seja, fizemos frações com denominador elevado desde o seu grau inicial 2 até o grau 1, nesse caso, foram só duas.
O numerador dessas frações que criamos sempre deve ter grau menor que o fator do denominador em uma unidade, como tem grau 2, seu numerador tem grau 1
Você t.em que lembrar que é como se tivéssemos , um termo de grau 1 repetido, então os numeradores das frações que vem desse termo devem ter grau 0. Beleza?
Vamos juntar os termos pelos graus de .
Como os denominadores já são os mesmos, temos
Vamos agora igualar cada coeficiente das potências de na esquerda e na direita. Como assim? Olha só:
Levando isso para nossa expressão de , temos:
Vamos tentar dar uma simplificada nisso aqui:
Passo 5
Agora vamos dar atenção às frações com denominador
Olhando para elas, não parecem nenhuma transformada conhecida, mas se tivesse só nós pensaríamos em um seno ou cosseno, não é? Vamos então fazer um pequeno algebrismo aqui para reconhecer esse seno.
Sempre que você encontrar um denominador desse tipo, você deve completar o quadrado do polinômio. Como assim? Vamos agrupar os termos que tem “” em um quadrado perfeito, olha só
Vamos fazer o mesmo para as frações que encontramos na decomposição parcial, ok? Temos então o seguinte
Passo 6
Precisamos, finalmente, reconhecer a função. Calma, tá acabando!
Repara o seguinte:
Essa é a transformada do seno em , agora vamos deslocar ela para :
A mesma coisa acontece para o cosseno!
Vamos substituir isso e:
Agora nós temos 2 problemas: essas transformadas em e essa exponencial que sobrou do lado de fora.
Para trazer a transformada para , vamos usar a seguinte fórmula:
Ou seja, só precisamos multiplicar o que está dentro de por :
Para resolver o problema da exponencial do lado de fora, precisamos dessa fórmula aqui:
Temos então
O que nos dá:
Finalmente: é o que está dentro dos colchetes