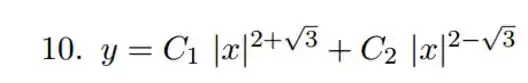![]()
![]()
Passo 1
Essa é uma EDO de Cauchy-Euler clássica. Perceba que ela está nesse formato aqui:
E sabemos que nesse caso basta que encontremos as raízes da equação
Passo 2
Então, no caso da nossa EDO
Então precisamos achar as raízes de
Que são
Passo 3
Uma vez encontradas as raízes, a solução da EDO para nosso caso, onde
Prontinho! Esse macete facilita ein?
Resposta