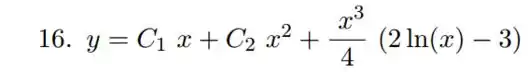![]()
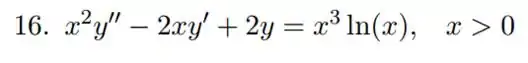
Passo 1
Vamos resolver essa EDO pelo método da variação de parâmetros. Para isso, a primeira coisa é resolver essa equação como se fosse homogênea, então vamos ignorar aquele termo ali do outro lado da igualdade rapidinho.
Tá no formatinho da EDO de Cauchy-Euler, vamos resolver por aquele macete que vai ser moleza.
Então
E nossas raízes vão ser
E a solução da EDO homogênea fica
Passo 2
Agooooora que vamos resolver a parte não homogênea. No método da variação de parâmetros
Onde vem da nossa solução homogênea. E calcula-se fazendo
E
é aquela função chatinha do outro lado a integral. Maaas atenção, precisamos pra isso da nossa EDO no formato
E nossa EDO é
Para deixar no formato do método precisamos dividir a equação inteira por , ficando com
Passo 3
Então vamos lá! Com a EDO no formato do método vamos encontrar essa solução particular!
Logo,
Então
Que se resolvido por partes fica
Já
Que também resolvendo por partes resulta em
Passo 4
Encontramos , agora podemos aplicar na nossa solução particular
Passo 5
Sabemos que a solução da EDO é
E
Logo, nossa solução é
Ufa! Finalmente!
Resposta