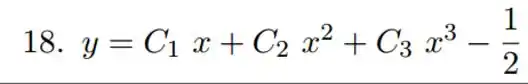![]()
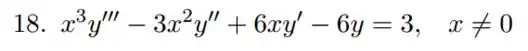
Passo 1
Olhando assim a gente vê uma equação bem complicada de resolver, mas vamos aplicar a substituição que ele sugeriu.
Lembrando que pra fazer essas derivadas temos que usar a regra da cadeia, beleza?
Da equação para podemos dizer que
Já da equação para podemos dizer que
Mas esse último termo é justamente , não é mesmo? Então
E como
Vamos olhar agora para a equação de
O último termo é enquanto que o segundo é três vezes , assim
Como , então
Substituindo os valores na EDO.
Agora nós temos uma EDO com coeficientes constantes não homogênea e podemos partir para a resolução.
Passo 2
O primeiro passo vai ser resolver a EDO homogênea associada.
Para isso vamos montar a equação característica.
Resolvendo a equação teremos.
Como só tivemos raízes de multiplicidade 1 e reais, a solução homogênea será.
Passo 3
Agora vamos calcular a solução particular. Vamos supor
Logo a solução particular será
E a solução geral será
Voltando para e .
Resposta