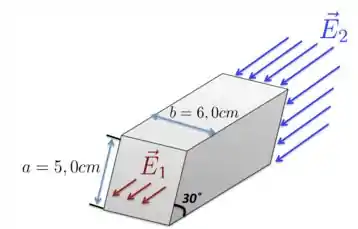
O campo elétrico em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico também é uniforme em todos os pontos e aponta perpendicularmente para dentro da face, como mostra a Figura abaixo. As duas faces mencionadas possuem uma inclinação de em relação à horizontal, enquanto e são, ambos, horizontais; o módulo de é igual a e o módulo de é igual a .
- Supondo que nenhuma outra linha de campo atravesse as superfícies do paralelepípedo, determine a carga líquida contida em seu interior.
- O campo elétrico existente é produzido somente pelas cargas no interior do paralelepípedo ou pode ser produzido também por cargas existentes fora dele? Como se pode ter certeza disso?
Passo 1
a) Sabemos, pela lei de Gauss, que o fluxo total do campo elétrico no vácuo é dado por
em que é a carga líquida no interior da superfície fechada .

Para gente matar essa questão, dá uma olhada na Figura acima, que representa a situação dada no exercício, mas desenhada de perfil. Blz? Assim facilita para a gente ver os ângulos entre os vetores e em cada face.
Seguindo de perto a Figura acima, repara que os vetores e têm o mesmo módulo, porque as duas faces têm mesma área, e ambos apontam perpendicularmente às respectivas faces, tranquilo??
Agora, como o campo elétrico em cada uma das faces é uniforme, ou seja, tem o mesmo valor em todos os pontos sobre a área de cada face, então, o fluxo para a face pode ser escrito como
e para a face
Lá da lei de Gauss, a gente pode escrever a carga líquida dentro do paralelepípedo como
Como e , a gente pode simplificar a expressão acima para
Jogando os valores dados no enunciado, chegamos a
o que mostra para a gente que a carga dentro do paralelepípedo é negativa. Por isso, parte das linhas de campo que vão para dentro dele terminam na carga . O restante das linhas vai para fora dele.
Passo 2
b) Ainda que tenha carga dentro, existe um campo elétrico que sai do paralelepípedo, o que significa que este campo vai terminar em alguma carga fora do paralelepípedo. Além disso, o campo é produzido por cargas do lado de fora do paralelepípedo.
O importante aqui é o seguinte: embora apenas a dentro da superfície fechada contribua para o fluxo elétrico através da superfície fechada do paralelepípedo, as cargas que estão fora continuam contribuindo para o campo elétrico na superfície fechada . Essa diferença é muito importante!!
Cargas elétricas fora da superfície fechada S produzem campo elétrico sobre essa superfície S, porém não contribuem para o fluxo elétrico total.
Resposta
- Cargas fora do paralelepípedo (que é a superfície fechada neste exercício!) contribuem para o campo sobre o paralelepípedo, mas não para o fluxo elétrico total !!