Suponha que exista uma superfície gaussiana fechada, cujo fluxo do campo elétrico é zero, para que isso seja verdade podemos dizer que:
- Existe a possibilidade de o campo elétrico ser nulo;
- Existe a possibilidade de não existir cargas em seu interior;
- Existe a possibilidade de em seu interior haver cargas elétricas, com a condição de serem dipolos elétricos
- Somente a afirmativa 3 está correta
- Somente as afirmativas 1 e 2 estão corretas
- Todas as afirmativas estão corretas
- Somente a afirmativa 1 está correta
- Somente a afirmativa 2 está correta
Passo 1
Primeiro vamos pensar no que a questão aborda, repara que ela fala em superfície gaussiana, falou nisso você pensa imediatamente na Lei de Gauss né? E qual é essa lei? A lei de Gauss nos diz que
Onde é a carga no interior da superfície gaussiana. Essa lei de Gauss nos dá o fluxo elétrico e para esse fluxo ser zero temos que ter os seguintes casos
Com isso a gente já ve que as alternativas 1 e 2 estão corretas. Agora você precisa pensar no que é um dipolo elétrico, vou te mostrar um desenho pra você ver como é um dipolo
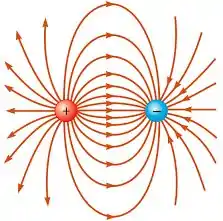
Então, um dipolo nada mais é que uma carga negativa unida com uma carga de mesmo módulo porém positiva, ou seja, a carga líquida é zero, então, no caso de um dipolo elétrico a carga no interior da superfície gaussiana também será zero, logo, não haverá fluxo elétrico. Então a alternativa 3 também esta correta. Todas as afirmativas estão corretas
Resposta
Todas as afirmativas estão corretas. Letra (c)