
Passo 1
a)
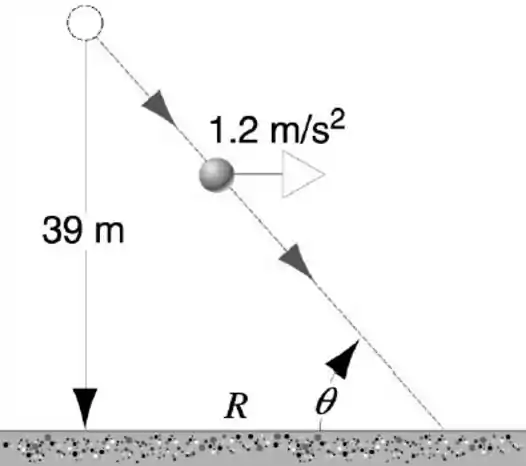
Primeiramente, vamos mostrar que a trajetória da bola é uma linha reta.
Vamos aplicar a equação do movimento uniformemente variado para o deslocamento:
Como a bola é largada, temos inicialmente uma velocidade nula.
Podemos calcular o deslocamento tanto para x quanto para y:
Em x, temos uma aceleração de . Aplicando a equação do MRUV, temos:
Em y, temos a aceleração da gravidade de . Aplicando a equação do MRUV, temos:
Agora podemos mexer um pouquinho nessas equações.
Substituindo na equação de x, chegamos a:
Podemos perceber que isso é a equação de uma reta.
Passo 2
a)
Continuando o item a, vamos calcular o deslocamento em x, ou seja, o valor de R.
Para isso, vamos achar o valor do tempo de queda da bolinha.
Sabemos que o deslocamento em y foi de 39. Aplicando a equação de y, chegamos a:
Agora é só substituir na equação do deslocamento em x:
Passo 3
a)
Agora do item a, falta o valor de .
Podemos ver que
Desenvolvendo:
Passo 4
b)
Para achar o tempo que a bola levar para atingir o solo é só calcular a raiz da equação que achamos no passo 2:
Passo 5
A velocidade que a bolinha atinge o chão será dada pela resultante da velocidade em x com a velocidade em y.
Aplicando e sabendo que , temos:
Calculando a resultante:
Resposta
![]()