Uma partícula se move sobre uma calha horizontal lisa com velocidade constante de módulo desconhecida. A calha horizontal transforma-se, suavemente, a partir do ponto A, em uma calha semicircular de raio R, tal como indicado na figura. Após percorrer toda a calha semicircular, a partícula deixa a calha no ponto B, que se encontra exatamente acima do ponto A, com velocidade horizontal de módulo v0 e cai de volta na calha horizontal em um ponto P. As calhas estão orientadas de modo que todo o movimento da partícula se passa num mesmo plano vertical. Considere desprezível o atrito entre a partícula e as calha em todos os momentos (entre os pontos A e B). Considere como dados do problema , e a aceleração da gravidade .
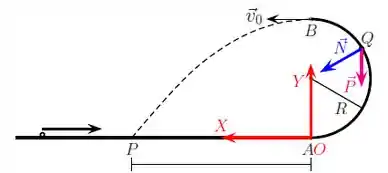
a) Faça um diagrama indicando as forças que atuam na partícula de massa quando ela passa pelo ponto Q, indicado na figura, localizado na calha semicircular.
b) Calcule a distância entre os pontos A e P.
c) Determine o vetor velocidade da partícula no instante imediatamente anterior a atingir novamente a calha horizontal, no ponto P. Indique claramente qual sua escolha para o sistema de eixos.
Passo 1
Na letra (a), queremos as forças sobre a partícula no ponto .
Quando a partícula passa pelo ponto , temos a força peso que sempre aponta para baixo e também a força normal que a calha exerce sobre a partícula na direção perpendicular à superfície de contato:
Passo 2
Na letra (b), queremos a distância entre e .
Essa distância é nada mais do que o alcance da partícula nesse lançamento horizontal que ela realiza a partir de .
Vamos chamar essa distância de .
Para descobrí-la, precisamos analisar tanto o movimento na vertical quanto na horizontal.
A partícula sofre apenas a aceleração da gravidade, que aponta verticalmente para baixo.
Assim, o movimento na vertical terá uma aceleração constante, enquanto o movimento na horizontal não terá aceleração nenhuma:
Passo 3
Olhando para o movimento na horizontal, temos que sua velocidade é constante (movimento uniforme).
Assim podemos usar:
Sua posição inicial em está na origem e sua velocidade na horizontal é o próprio :
Então, para descobrir a distância que a partícula percorre na horizontal, basta descobrir o tempo que dura o movimento e substituir nessa expressão.
Passo 4
Olhando para o movimento na vertical, temos uma aceleração constante (), então podemos usar:
Sua posição inicial em é igual a duas vezes o raio do looping:
Sua velocidade inicial em é nula:
Além disso, a sua aceleração é a aceleração da gravidade e aponta no sentido negativo do eixo (para baixo).
Juntando tudo, ficamos com:
Passo 5
Queremos saber o tempo até a partícula atingir o chão.
Então, vamos substituir a posição em por (altura do chão):
Passo 6
Agora que sabemos o tempo que a partícula leva até o chão, basta substituir na equação de movimento na horizontal para descobrir a distância :
Passo 7
Na letra (c), queremos saber o vetor velocidade no momento em que a partícula chega ao chão.
A partícula terá uma componente horizontal e uma vertical:
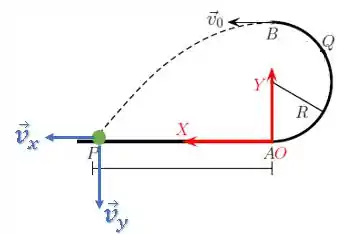
A componente horizontal nós já conhecemos pois ela não muda durante o movimento (aceleração apenas na vertical), então:
Já a componente vertical, nós vamos calcular.
A velocidade no MUV é calculada com:
Substituindo o intervalo de tempo que já achamos no PASSO 5, temos:
Passando para dentro da raiz elevado ao quadrado:
Ahh e esse sinal de negativo é uma questão de referencial...
Nosso sistema de eixos é com para cima, então a velocidade será negativa pois está para baixo.
Agora é só juntar as componentes e já temos nosso vetor velocidade:
Resposta
(a)
(b)
(c)