UFCG – Sem campus – Cálculo Diferencial e Integral I – Listas de cálculo 1 – UAMat – Lista 1 – Limite e continuidade – 10g
Calcule os limites
g)
Passo 1
Fala turminha, tudo em cima? Vamo pra questão. Ela nos dá um limite vindo de uma divisão de dois polinômios do seguinte jeito:
O que será que acontece se a gente aplicar o limite da forma como está?
Temos que:
Aplicando:
Caímos numa indeterminação do tipo , sabíamos que não iria ser fácil... mas não é impossível! Pra esses casos de divisões de polinômios gerando alguma indeterminação, sempre procure deixar o polinômio do numerador e/ou denominador de outra forma, a fim de tirar a indeterminação do denominador igual a 0.
Ou seja, temos de achar algum jeito de o nosso numerador se simplificar com o denominador, mudando a cara deles... dando um tapinha no visual. Vem comigo?
Passo 2
Show, então nosso limite tem essa cara:
Vamos começar mudando um pouco a cara do denominador, sempre é legal ver o porque dele está chegando a primeiro. O polinômio é dado por:
Você sabe como podemos reescrever ele? Isso mesmo, na forma:
Sendo e as raízes. Pra gente achar as raízes dela, vamos aplicar Bhaskara! Inclusive se você já sabe aplicar a regra de Bhaskara, lhe convido a achar as raízes antes de mim e depois conferir se deu tudo certo! Vamo seguindo:
Por Bhaskara, temos que:
Do nosso polinômio:
Temos:
Calculando as raízes:
Ou seja, nosso polinômio:
Pode ser reescrito como:
Ou,
Voltando para o nosso limite:
Olha só o safadinho ali! A nossa indeterminação acontece por conta desse , que quando levado ao limite, resulta em e anula todo o resto do denominador. E temos que sumir com ele... como fazemos isso? No próximo passo eu te mostro!
Passo 3
Belezura, nosso limite agora tem a seguinte cara:
E lembra da nossa dica de ouro? No denominador aparece o termo que faz tudo dar errado . Devemos então dar uma forma de simplificar o numerador de forma que em cima apareça também um , somente dessa forma conseguiremos desenvolver! Sabendo disso, inferimos que uma das raízes desse nosso polinômio de grau , é . Vamos testar isso? Aplicando em:
Obtemos:
Ou seja, realmente é uma raiz desse nosso polinômio, mas para reescrevemos ele, precisamos das duas outras raízes. Felizmente um camarada chamado Girard, descobriu umas relações bem interessantes com as três raízes de um polinômio de grau 3. Elas são:
Sendo esses coeficientes e , os coeficientes dos termos de um polinômio de grau 3 da seguinte forma:
Para o nosso polinômio:
Temos que e .
Portanto, das relações de Girard:
E olha que bacana, já sabemos uma das raízes, , portanto:
Dessa temos um sistema que podemos encontrar as outras duas raízes!
Entenderam a ideia? No próximo passo eu continuo com o sistema pra vocês
Passo 4
Do nosso sistema,
Conseguimos encontrar as outas raízes. Primeiro isolando na equação :
Aplicando isso na equação :
E, aplicando isso na equação :
Perfeito! Então nossa equação da parte superior que antes era:
Agora pode ser reescrita como:
Ou seja, nosso limite agora tem a cara:
Opa, aqui conseguimos fugir! Simplificando aqueles 2 termos iguais:
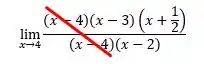
Ihuuul! Agora é só aplicar o valor do limite:
E é isso gente boa, matamos a questão! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você