UFCG – Sem campus – Cálculo Diferencial e Integral I – Listas de cálculo 1 – UAMat – Lista 1 – Limite e continuidade – 10h
Calcule os limites
h)
Passo 1
Fala aí meus bacanos, tudo em cima? A questão pede pra gente resolver o seguinte limite:
Ué, sem problemas! Vamos aplicar o limite e investigar o que acontece:
Aplicando
Poisé galera, caímos em uma indeterminação. Mas sem problemas... podemos sair dela, tentando reescrever esses polinômios de uma forma diferente. Você tem alguma dica de como proceder? Bem, vamos começar nossa análise. Primeiro temos que observar que estamos trabalhando com uma divisão de polinômios.
E que quando levados ao valor de , ambos polinômios retornam pra gente o valor . Isso significa uma coisa muito útil pra gente: é raiz de ambos os polinômios. Mas, no que isso ajuda a gente? Veja, a gente pode reescrever esses dois polinômios sabendo que é uma das raízes! No próximo passo te mostro isso melhor
Passo 2
Show, te falei que a gente pode reescrever esses polinômios. Vamos começar pelo denominador que é mais simples? Ele é um polinômio de segundo grau, de formato:
E pode ser reescrito nesse formato:
Sendo e as duas raízes dele. Para acharmos essas raízes, vamos aplicar Bhaskara, você lembra como aplicamos essa equação? Temos que:
Para nosso polinômio:
Calculando as raízes:
Ou seja, nosso polinômio pode ser reescrito como:
Inclusive comprovamos que é de fato uma raiz. Agora vamos pro numerador!
Passo 3
Aqui no numerador o “buraco é mais embaixo”. O que rola é o seguinte: já que sabemos uma das raízes e precisamos reescrever esse polinômio em um outro formato:
Sendo um polinômio de grau 5 e um polinômio de grau 4.
Lembrando que sabemos quem é , que representa uma das raízes da função. E achamos que , portanto:
E olha que bacana fica o nosso limite:
Desenvolvendo ele:
Agora só precisamos achar quem é esse .Sabe qual o método que vamos usar para encontra-lo? O método que vai nos mostrar como acontece isso é o método de Briot-Rufini.
Se liga que vou te mostrar como ele funciona:
Primeiro passo do Briot-Rufini é armar ela. Se temos uma equação do tipo:
E já sabemos uma das raízes , podemos montar da seguinte forma:
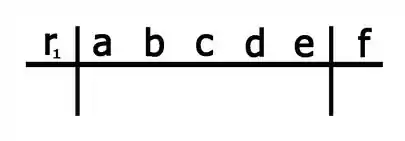
Como nosso polinômio é:
Temos que os coeficientes são:
Montando no Briot-Rufini:
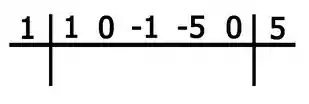
Show, e agora vem a dinâmica: Primeira coisa é descer o primeiro coeficiente!
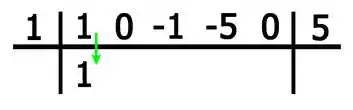
Agora, para encontrarmos os próximos coeficientes, realizaremos:
O produto do último novo coeficiente que achamos, com a raiz , somados com o próximo coeficiente.
Pra ficar mais fácil, visualmente temos:
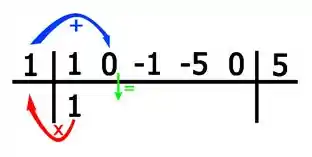
Ou seja:
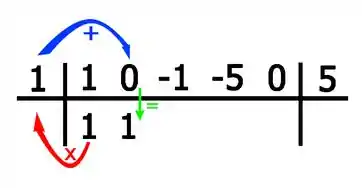
E por aí vai. Continuando o método:
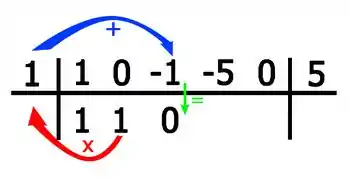
Para o próximo coeficiente:
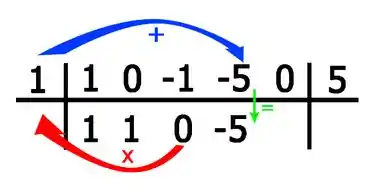
Para o próximo coeficiente:
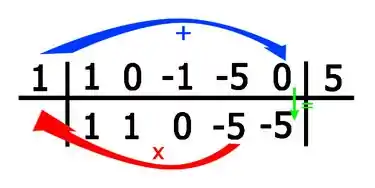
E por fim para a constante:
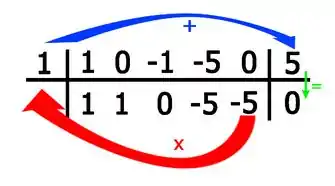
Belezura, de posse desses novos coeficientes , podemos escrever uma nova função da forma:
Usando os novos coeficientes que obtemos do método:
Passo 4
Estamos quase lá!! De começo, após simplificar numerador e denominador, obtivemos:
E encontramos que:
Agora não tem jeito, é aplicar o limite! Temos então que, aplicando o limite:
Ou seja:
E é isso gente boa, matamos a questão! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você