Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Aplicações da Hidrodinâmica

Ver Teoria
Exercício 451234567891011121314151617181920212223242526272829303132333435363738394041424344464748

Enunciado

O tubo horizontal mostrado na figura abaixo tem uma seção transversal de área de A 1 = 20 c m 2 na parte mais larga e A 2 = 10 c m 2 na parte mais estreita, como indicado na figura. A água está escoando pelo tubo com uma vazão de 6 × 10 - 3 m 3 / s . Esse tubo é conectado a outro tubo em formato U, contendo uma coluna de mercúrio. Ache:

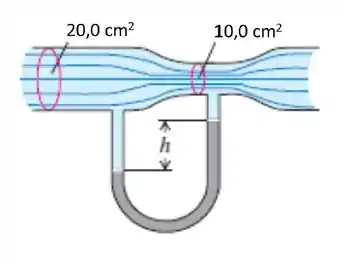
(a) A velocidade de escoamento na parte mais larga v 1 e na parte mais estreita v 2 .

(b) A diferença de pressão entre essas duas localizações considerando pontos de mesma altura.

(c) A diferença de altura h entre as colunas de mercúrio no tubo em formato de U.

Dados:

ρ á g u a = 1 × 10 3 k g / m 3

ρ m e r = 13,5 × 10 3   k g / m 3

g = 10 m / s 2

Passo 1

Pra achar essa velocidade temos que lembrar que a vazão em volume é dada por

V = A v

Na parte mais larga temos que v 1 será dada por

v 1 = V A 1 = 6 × 10 - 3 20 × 10 - 4

v 1 = 3 m / s

Já na parte mais estreita

v 2 = V A 2 = 6 × 10 - 3 1 0 × 10 - 4

v 2 = 6 m / s

Lembrando que A 1 = 10 c m 2 = 10 10 - 2 m 2 = 10 × 10 - 4 m 2 e A 2 = 2 0 c m 2 = 2 0 10 - 2 m 2 = 2 0 × 10 - 4 m 2 .

Passo 2

Para calcular a diferença de pressão podemos usar a equação de Bernoulli

ρ g h 1 + 1 2 ρ v 1 2 + p 1 = ρ g h 2 + 1 2 ρ v 2 2 + p 2

Como os dois pontos estão a mesma altura h 1 = h 2

1 2 ρ v 1 2 + p 1 = 1 2 ρ v 2 2 + p 2 → p 1 - p 2 = 1 2 ρ v 2 2 - v 1 2 = 1 2 10 3 6 2 - 3 2

p 1 - p 2 = 1,35 × 10 4   P a

Passo 3

Do lado esquerdo do tubo em U na interface água/mercúrio a pressão é dada por

p e s q = p 1 + ρ á g u a g ( h + x )

Onde p 1 é a pressão acima dessa interface onde tem vazão do fluido e x + h é a altura dessa coluna de água até o ponto onde a pressão é p 1

Já a pressão do lado direito do tubo em U, a mesma altura da interface água/mercúrio do lado esquerdo é dada por

p d i r = p 2 + ρ m e r g h + ρ á g u a g x

Onde h é a altura da coluna de mercúrio em relação ao nível da interface água/mercúrio, como na figura, e x   é a altura da coluna de água acima da coluna de mercúrio.

Pelo princípio de Stevin

p e s q = p d i r

p 1 + ρ á g u a g h + x = p 2 + ρ m e r g h + ρ á g u a g x

p 1 + ρ á g u a g h + ρ á g u a g x = p 2 + ρ m e r g h + ρ á g u a g x

p 1 - p 2 = g h ρ m e r - ρ á g u a

h = p 1 - p 2 g ρ m e r - ρ á g u a = 1,35 × 10 4 10 × 13,5 × 10 3 - 1 × 10 3

h = 1,08 × 10 - 1 m

Resposta

(a)

v 1 = 3 m / s

v 2 = 6 m / s

(b)

p 1 - p 2 = 1,35 × 10 4   P a

(c)

h = 1,08 × 10 - 1 m

Exercícios de Livros Relacionados

A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo A B C deve estar inicialmente cheio, mas, se essa condição é satisfeita, o líquido escoa pelo
Uma transição abrupta ocorre nos números de Reynolds de cerca de 3 * 10 5 , onde o arrasto em uma esfera se move através de um fluido diminui abruptamente. Estimar a velocidade com que essa transição
O cano de saída do esgoto de uma casa construída em uma encosta está a 6,59m abaixo do nível da rua. Se o cano coletor do esgoto está 2,16m abaixo do nível da rua, calcule a menor diferença de pressão
Qual é a área mínima (em metros quadrados) da supefície superior de uma placa retangular de gelo com 0,441m de espessura que flutua na água doce para que seja capaz de sustentar um automóvel de 938k g
A água flui através de um tubo horizontal de 25,0 cm de comprimento um diâmetro interno de 1,20 mm em 0,300 mL/s. Encontre a diferença de pressão necessária para conduzir esse fluxo se a viscosidade d