Um bloco encontra-se na iminência de deslizamento sobre um plano inclinado que forma um ângulo com a horizontal. Qual é o valor do coeficiente de atrito estático ?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Quais são as forças sobre o bloco?
Temos a força peso que puxa o bloco para baixo da rampa. A força de atrito está atuando contra essa tendência de deslizar para baixo, então , ela aponta para cima da rampa.
Além disso, temos uma força normal perpendicular à rampa:
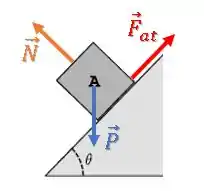
Como o bloco está na iminência de deslizar, sua força de atrito é máxima e vale:
Podemos achar o valor do coeficiente de atrito estático através das equações de equilíbrio do bloco.
Passo 2
Vamos decompor a força peso:
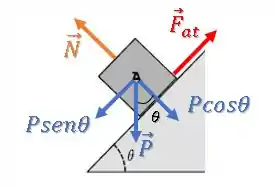
Como o bloco está em equilíbrio, o somatório de forças ao longo da direção perpendicular e paralela à rampa é nulo:
Substituindo o valor da , temos:
Um jeito bem direto de resolver esse sistema é dividindo a equação de baixo pela equação de cima:
Opaa, como o ângulo é , já encontramos o coeficiente de atrito:
Com aquela tabelinha dos ângulos notáveis que temos no sangue já, achamos que:
Resposta
Letra (c)