[ENUNCIADO COMUM ÀS QUESTÕES 10 e 11]
Considere o seguinte experimento para medirmos o coeficiente de atrito estático entre duas superfícies. Colocamos um bloco sobre um plano inclinado cuja inclinação podemos controlar. Inicialmente o plano está na horizontal. Lentamente, aumentamos o ângulo entre o plano e a horizontal, como na figura. Sobre essa situação responda as questões 10 e 11.
[QUESTÃO 10]
Observamos que o bloco começa a se mover quando o ângulo é . Qual dos valores abaixo melhor aproxima o coeficiente de atrito estático entre as superfícies?
(A)
(B)
(C)
(D)
(E)
Passo 1
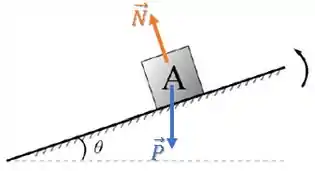
Vamos olhar para as forças sobre o bloco.
Temos uma força peso e normal:
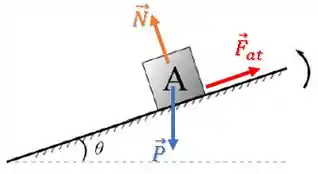
Como a tendência de deslizamento do bloco é para baixo da rampa, temos uma força de atrito para cima da rampa:
Passo 2
Okay, mas o que o ângulo de inclinação muda nessa história?
Bom, podemos decompor a força peso em duas componentes (paralela e perpendicular à rampa) usando o ângulo .
Fazendo aquela manipulação que sempre fazemos nos planos inclinados, o ângulo aparece alí:
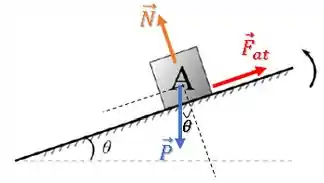
Assim, as componentes são:
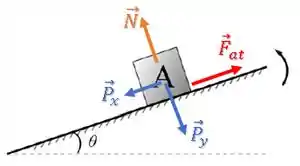
A componente é responsável por “puxar” o bloco para baixo da rampa.
Então, conforme o ângulo vai aumentando, temos que vai aumentando também, até que a força de atrito não é mais capaz de manter o bloco em equilíbrio.
Passo 3
Fazendo o equilíbrio de forças, temos:
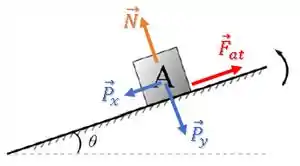
Na direção da rampa:
Na direção perpendicular à rampa:
Passo 4
A força de atrito vai conseguir manter o bloco em equilíbrio até que ela atinja seu valor máximo:
Nessa situação limite, temos que:
Passo 5
Ficamos com um sistema assim:
Nosso objetivo é achar o coeficiente de atrito ...
Existem diferentes maneiras de se resolver o sistema, uma delas é dividir a primeira equação pela segunda:
Passo 6
A situação limite acontece quando o ângulo é de , logo:
Podemos aproximar por :
Ficamos com a letra (C).
Resposta
Letra (C)