Um bloco de massa está sobre uma mesa horizontal sendo empurrado em movimento retilíneo por uma força constante dada, com velocidade e aceleração de mesmo sentido que a força; o coeficiente de atrito cinético entre o bloco e a mesa é . Sobre esse primeiro bloco há um segundo bloco de mesma massa e rigidamente colado ao primeiro, como indica a figura.
a) Faça um diagrama de forças externas sobre o sistema constituído pelos dois blocos;
b) Calcule o módulo a da aceleração com a qual os blocos se deslocam;
c) Calcule os módulos da força horizontal e da força vertical que o bloco exerce sobre o bloco .
Passo 1
a)
Ele pediu o diagrama das forças sobre o sistema composto pelos 2 blocos. É como se fosse um bloco só de massa .
Então as forças atuando no sistema são a força peso , a força normal da superfície , a força e a força de atrito . O diagrama de forças fica: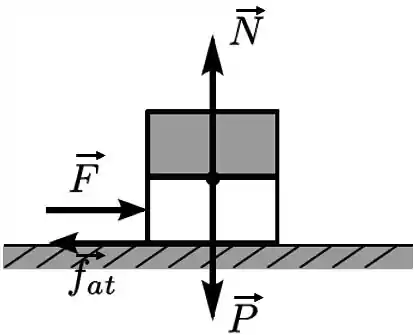
Passo 2
b)
Vou fazer uma observação antes da gente começar as contas: sempre que eu botar um vetor sem a flechinha é porque eu estou falando do módulo do vetor, beleza? Tipo, é o módulo de . Dito isso, vamos continuar :)
Passo 3
O bloco não tem nenhum movimento no eixo vertical, então, pela 2ª lei de Newton, as forças nesse eixo se cancelam:
Passo 4
Agora vamos aplicar a 2ª lei de Newton no eixo horizontal. As forças atuando nele são a e a , então, sendo o vetor aceleração dos blocos:
E como os blocos andam pra direita:
Passo 5
E o módulo da força de atrito é:
lembrando que é o coeficiente de atrito cinético.
Vimos que , então
Passo 6
Mas a gente quer achar a aceleração! Então vamos substituir esse valor de na equação que achamos antes
Aí dá:
Show! Vamos pra letra (c)!
Passo 7
c)
Vamos focar no bloco , ver quais forças estão atuando nele.
Pra começar, tem sua força peso . Tem também a força normal, que é justamente a força vertical que o bloco faz no bloco , e que a gente quer achar o módulo!
Então vamos chamar essa força normal de .
Passo 8
Mas o bloco anda pra direita, então tem que ter uma força empurrando ele pra lá. A força só empurra o , mas como os 2 blocos estão colados, o bloco acaba indo junto também.
Essa força da cola que faz o bloco ir pra direita junto com o bloco é uma forma de força de atrito também, que é justamente a força horizontal do bloco sobre o bloco que ele pediu. Então vamos chamar essa força de .
Passo 9
Portanto, o diagrama de forças atuando no bloco é:
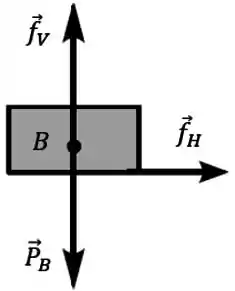
Passo 10
Não há movimento no eixo vertical então, pela 2ª lei de Newton:
Esse é o módulo da força vertical que o bloco exerce no bloco .
Passo 11
E no eixo , a 2ª lei de Newton fica:
Essa aceleração é a mesma que vimos na letra (b), então
Esse é o módulo da força horizontal que o bloco faz no .
Resposta
a)
b)
c)