A figura seguinte representa um sistema formado por duas cunhas e , ambas com massa igual a , sobre uma superfície horizontal perfeitamente lisa; não há contato entre a cunha e essa superfície horizontal. O coeficiente de atrito estático entre as superfícies das cunhas é igual a . Sob ação de uma força horizontal constante, aplicada em , como mostra a figura, o sistema se move em movimento retilíneo uniformemente acelerado, sem que a cunha deslize sobre a cunha . O módulo de e demais condições são tais que o atrito entre as cinhas tem que impedir a cunha de deslizar para cima sobre a . Considere como dados , , , o ângulo indicados na figra e a aceleração da gravidade .
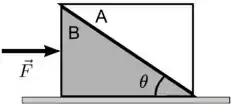
- Determine a força resultante sobre a cunha .
- Calcule o módulo da força total que a cunha exerce sobre a cunha .
- Represente em um diagrama todas as forças que agem sobre cada uma das cunhas.
- Calcule o módulo da força de atrito entre as cunhas.
- Determine a máxima intensidade da força aplicada , de modo que a cunha ainda não suba deslizando sobre a cunha .
Passo 1
Primeiro vamos escrever os dados do enunciado
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Passo 2
a)
Antes de fazer o DCL de cada bloco, vamos fazer algo que facilita nossas contas, o DCL do sistema. Considerando e uma coisa só.
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Não, não existe mola atuando.
Não, o sistema não possui atrito.
O DCL do sistema fica
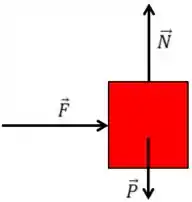
Passo 3
No , temos
Atenção!!!
Usamos a massa do sistema na fórmula da força resultante
Passo 4
Usando a fórmula da força resultante para a cunha temos
Passo 5
b)
Vamos agora fazer o DCL da cunha
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o sistema está apoiado no outro bloco.
Não, não existe fio atuando.
Não, não existe mola atuando.
Sim, existe atrito entre as cunhas.
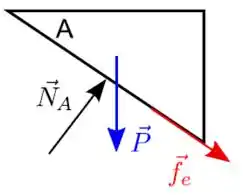
Passo 6
Diferente do normal, vamos escrever essa soma vetorialmente, em vez de cada componente das forças
Ele pede a reação do chão, lembra que ela é a soma da força normal coma força de atrito?
Repara que a força resultante é para direita, enquanto é para cima, isso nós diz que
O módulo da reação vai ser
No caso o “chão” é a cunha .
Passo 7
Vamos agora fazer o DCL da cunha
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o sistema está apoiado no outro bloco e no chão.
Não, não existe fio atuando.
Não, não existe mola atuando.
Sim, existe atrito entre as cunhas.
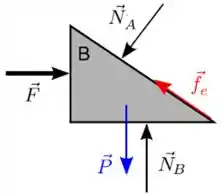
Passo 8
c)
Vamos fazer um esquema das forças na cunha para entendermos direito onde fica cada ângulo
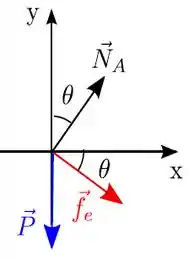
O ângulo é o ângulo da junção com a horizontal, como a força de atrito está na horizontal, aquele ângulo da força de atrito com a horizontal deve ser .
A força normal é perpendicular a força de atrito, isso nós diz que enquanto o ângulo da força de atrito é na horizontal, o ângulo da normal será com a vertical.
Passo 9
Vamos começar fazendo o equilíbrio ao longo do ,
Devemos encontrar usando a “regra do COlado, SEparado”.
Devemos encontrar usando a “regra do COlado, SEparado”.
Vamos ter
Lembre que a força de atrito estática NÃO é dada pela fórmula. O que a fórmula nos diz é a força de atrito MÁXIMA.
Passo 10
Essa fórmula não resolve nada, então vamos fazer a analise no
Devemos encontrar usando a “regra do COlado, SEparado”.
Devemos encontrar usando a “regra do COlado, SEparado”.
Lembrando que
Passo 11
Encontramos
Esse sistema não é muito fácil de resolver, mas vamos lá
Multiplicando a primeira equação por e a segunda equação por
Fizemos isso para igualar os caras que multiplicam a normal. Porque fizemos isso? Quando somarmos as equações as forças normais vão se anular. Vamos somar os dois lados para ver isso
Lembre que
Vamos ter
Passo 12
e)
A força máxima acontece quando a força de atrito for máxima, que a situação limite para as cunhas se moverem juntas
Vamos reescrever as equações para a cunha
Nessa situação limite
Substituindo
Passo 13
Da primeira equação
Da segunda equação
Igualando isso
Complexa essa questão. Recomendo que você a reveja desde o início com muita calma, mesmo que tenha entendido. É importante fixar bem essa questão.!!!