Exercícios de Atrito Estático - Lista de Exercícios Resolvida
Questão 1
Se você pressiona um caixote de maçãs contra uma parede com tanta força que o caixote não escorrega parede abaixo, qual é a orientação (a) da força de atrito estático que a parede exerce sobre o caixote e (b) da força normal que a parede exerce sobre o caixote? Se empurra o caixote com mais força, o que acontece (c) com e (d) com ?
Ver solução completaQuestão 2
Bagagens são transportadas de um local a outro de um aeroporto por uma esteira . Em um certo local a esteira tem uma inclinação de com a horizontal. Suponha que para o ângulo tão pequeno as malas não escorreguem. Determine o módulo da força de atrito exercida pela esteira sobre uma caixa de de peso quando a caixa está na parte inclinada da esteira e a velocidade da esteira é (a) nula e constante, (b) e constante, (c) e aumentando a uma taxa de e (d) e diminuindo a uma taxa de e (e) e aumentando a uma taxa de . (f) Para quais dessas cinco situações a força de atrito é dirigida para baixo ao longo da rampa?
Considere que quando a mala sobe a sua velocidade é positiva.
Ver solução completaQuestão 3
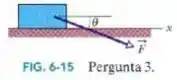
Na Fig. 6-15, se a caixa está parada e o ângulo entre a horizontal e a força aumenta, as grandezas a seguir aumentam, diminuem ou permanecem com o mesmo valor: (a) ; (b) ; (c) ; (d) ?
Questão 4
Em três experimentos, três forças horizontais diferentes são aplicadas ao mesmo bloco que está sobre a mesma bancada. Os módulos das forças são e . Em cada experimento o bloco permanece estacionário, mesmo com a aplicação da força. Ordene as forças, em ordem decrescente, de acordo (a) com o módulo da força de atrito estático que a bancada exerce sobre o bloco e (b) com o valor máximo dessa força.
Ver solução completaQuestão 5
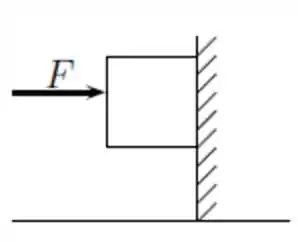
Uma força horizontal , de módulo 40 N, empurra um bloco de peso 30 N contra uma parede vertical. O coeficiente de atrito estático entre a parede e bloco é 0,80 e o de atrito cinético é 0,60. Suponha que inicialmente o bloco esteja em repouso. A sentença correta é
(a) O bloco começará a se mover e o módulo da força resultante exercida pela parede sobre o bloco vale 32 N;
(b) O bloco começará a se mover e o módulo da força resultante exercida pela parede sobre o bloco vale 51,2 N;
(c) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 70 N;
(d) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 50 N;
(e) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 30 N;
Questão 6
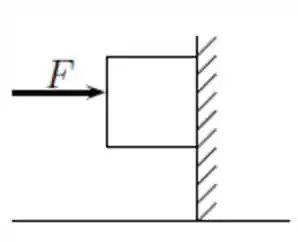
Uma força horizontal , de módulo 40 N, empurra um bloco de peso 30 N contra uma parede vertical. O coeficiente de atrito estático entre a parede e bloco é 0,80 e o de atrito cinético é 0,60. Suponha que inicialmente o bloco esteja em repouso. A sentença correta é
(a) O bloco começará a se mover e o módulo da força resultante exercida pela parede sobre o bloco vale 32 N;
(b) O bloco começará a se mover e o módulo da força resultante exercida pela parede sobre o bloco vale 51,2 N;
(c) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 70 N;
(d) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 50 N;
(e) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 30 N;
Questão 7
A figura seguinte representa um sistema formado por duas cunhas e , ambas com massa igual a , sobre uma superfície horizontal perfeitamente lisa; não há contato entre a cunha e essa superfície horizontal. O coeficiente de atrito estático entre as superfícies das cunhas é igual a . Sob ação de uma força horizontal constante, aplicada em , como mostra a figura, o sistema se move em movimento retilíneo uniformemente acelerado, sem que a cunha deslize sobre a cunha . O módulo de e demais condições são tais que o atrito entre as cinhas tem que impedir a cunha de deslizar para cima sobre a . Considere como dados , , , o ângulo indicados na figra e a aceleração da gravidade .
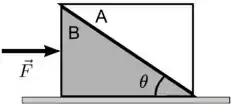
- Determine a força resultante sobre a cunha .
- Calcule o módulo da força total que a cunha exerce sobre a cunha .
- Represente em um diagrama todas as forças que agem sobre cada uma das cunhas.
- Calcule o módulo da força de atrito entre as cunhas.
- Determine a máxima intensidade da força aplicada , de modo que a cunha ainda não suba deslizando sobre a cunha .
Questão 8
Três blocos de massa , e estão dispostos como visto na figura abaixo. Atua no bloco de massa uma força externa , horizontal e de módulo que faz o conjunto de blocos se movimentar. O bloco de massa não escorrega sobre o bloco de devido ao atrito estático atuando na interface entre estes dois blocos. Não existe atrito entre os blocos de massa e com o solo. Considerando a aceleração da gravidade determine:
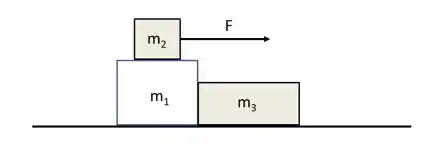
Os diagramas das forças que atuam em cada um dos três blocos;
A aceleração do bloco de massa ;
A força que o bloco de massa faz no bloco de massa ;
O coeficiente de atrito estático entre os blocos de massas e .
Ver solução completaQuestão 10
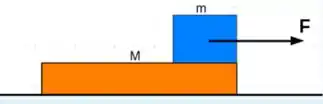
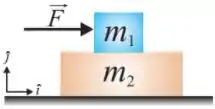
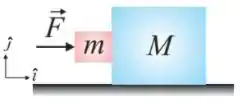
Uma caixa de massa é colocada em cima de uma caixa maior de massa como mostrado na figura. Quando uma força de módulo é aplicada na caixa grande, ambas as caixas se movem para a direita com a mesma aceleração. Supondo que o coeficiente de atrito entre as caixas é e que não há atrito entre a caixa maior e ochão, qual é a força atuando na massa menor?
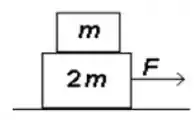
Questão 11
Uma força horizontal empurra um bloco de massa contra uma parede vertical. O coeficiente de atrito entre o bloco e a parede é . Qual é o módulo mínimo da força que é necessário para manter o bloco sem escorregar para baixo no muro?
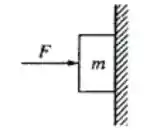
Questão 12
Você está segurando um livro contra uma parede vertical aplicando uma força com sua mão. O ângulo entre sua força e a vertical é , como mostra a figura abaixo. A massa do livro é e o coeficiente de atrito estático é . Se você empurrar forte demais, o livro começará a deslizar para cima e se você não aplicar força suficiente, o livro deslizará para baixo.
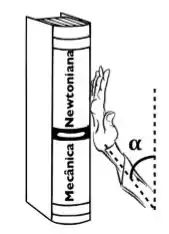
Esboce o diagrama de forças para os dois casos na situação em que o livro está prestes a deslizar.
Calcule a magnitude da força que você deve aplicar (como função de ) na iminência do movimento, também nos dois casos.
Calcule a magnitude da força aplicada (como função de ) para a qual a força de atrito se anula. Avalie o resultado para e .
Para um dado ângulo de aplicação da força, determine o intervalo de valores de em que ainda é possível fazer com que o livro deslize para cima.
Ver solução completaQuestão 13
Considere as polias e as cordas ideais para o dispositivo da figura abaixo. Despreze suas massas e o atrito das cordas com as polias. Como a polia que sustenta o bloco 2 é móvel, o módulo da aceleração do bloco 1 equivale ao dobro do módulo da aceleração do bloco 2. Adote os valores para as massas dos blocos e . A inclinação do plano é . Não há atrito entre o bloco 1 e o seu plano de apoio. Utilize .
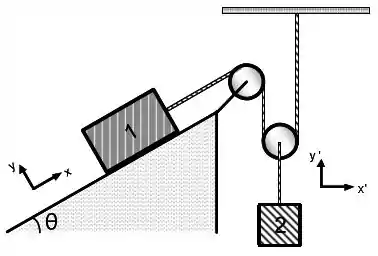
a) Represente o diagrama do corpo livre e escreva as equações de movimento em termos de suas componentes para os dois blocos e a polia móvel presa ao bloco 2. Utilize os sistemas de coordenadas fornecidos para cada componente do sistema.
b) Calcule o vetor aceleração de cada um dos blocos, usando como referência o sistema de coordenadas convencional apresentado para o bloco 2.
c) Considere agora que há atrito entre o bloco 1 e sua superfície de apoio. Reescreva as equações de movimento e determine o coeficiente de atrito mínimo necessário para que o sistema se mantenha em repouso.
Ver solução completaQuestão 14
Um bloco de massa está sobre o solo, quando passa atuar sobre ele uma força de módulo que faz um ângulo com a horizontal, conforme mostra a figura. Os coeficientes de atrito estático e cinético entre o bloco e o solo são e respectivamente. Utilize .
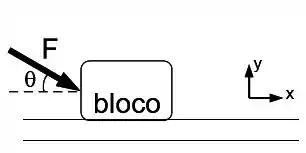
a) Que tipo de força de atrito age sobre o bloco? Determine esta força. Utilize o sistema de coordenadas indicado na figura e seus respectivos vetores unitários para a sua resposta.
Agora o mesmo bloco é agora colocado sobre uma prancha de massa e ambos são colocados sobre uma mesa com atrito desprezível. A mesa não é mostrada na figura. O coeficiente de atrito estático entre o bloco e a prancha é . O sistema entra em movimento quando uma força horizontal de módulo atua sobre a prancha conforme mostra a figura. Não há movimento relativo entre o bloco e a prancha.
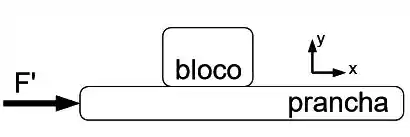
b) Faça um diagrama de corpo livre para o bloco e para a prancha. Indique de forma clara nos diagramas que forças constituem pares ação-reação.
c) Escreva as equações de movimento em termos das suas componentes para o bloco e para a prancha. Utilize o sistema de coordenadas indicado na figura.
d) Calcule o valor máximo de para que não haja movimento relativo entre o bloco e a prancha. Calcule a aceleração do conjunto para este caso.
Ver solução completaQuestão 17
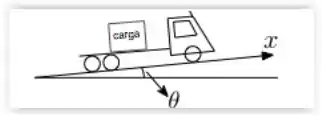
Um caminhão de carga sobe uma rua de inclinação θ com relação à horizontal, conforme indicado na figura. Uma carga de massa m encontra-se apoiada sobre a carroceria do caminhão sem deslizar. Os coeficientes de atrito estático e cinético entre a carga e a carroceria do caminhão são µe e µc, respectivamente. Sabendo que o caminhão sobe a rua com velocidade constante, qual é a magnitude da força de atrito que atua sobre a carga ?
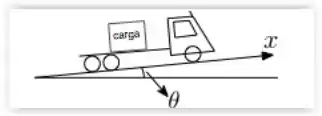
(A)
(B) = mg sen()
(C ) = mg cos()
(D) = µe mg sen()
(E) = µe mg cos()
Ver solução completaQuestão 18
Dois blocos retangulares idênticos são posicionados de duas maneiras diferentes sobre um plano inclinado: (i) é colocado no plano inclinado sobre o seu lado mais longo e (ii) é colocado no plano inclinado sobre o seu lado mais curto. Ambos os casos estão ilustrados na figura abaixo. O bloco colocado sobre o seu lado mais curto desliza no plano inclinado enquanto o bloco colocado sobre o seu lado mais longo permanece em repouso. Quais das afirmações abaixo é capaz de melhor explicar este fenômeno:
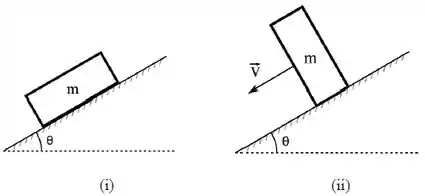
(a) O lado mais curto do bloco é menos rugoso do que o lado mais longo, aumentado consideravelmente o coeficiente de atrito estático no caso (i).
(b) A força de atrito depende fortemente da área de contato do bloco com a superfície, levando a uma força de atrito muito menor no caso (ii).
(c) O centro de gravidade no caso (ii) é mais alto.
(d) A força normal é menor no caso (ii).
(e) A componente da força gravitacional na direção paralela à superfície do plano inclinado é maior no caso (ii).
Ver solução completaQuestão 19
Uma vassoura de massa é empurrada por um chão áspero horizontal com uma força de magnitude aplicada com um ângulo , como mostrado acima. O coeficiente de atrito entre a escova e o piso é . A força de atrito sobre a vassoura tem magnitude:
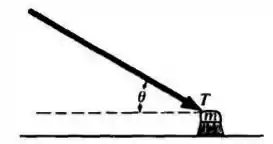
a)
b)
c)
d)
e)
Ver solução completaQuestão 20
Um elevador de carga está se movendo verticalmente. Sobre seu piso horizontal encontram-se um caixote muito pesado e um operário, ambos em repouso em relação ao elevador, como mostra a figura. Em um dado instante, o operário empurra o caixote e percebe que a intensidade da força horizontal que ele precisou exercer para fazer o caixote começar a deslizar sobre o piso é menor do que a intensidade da força horizontal que ele precisaria exercer para fazê-lo começar a deslizar quando o elevador estava em repouso. Qual das seguintes afirmativas é correta?
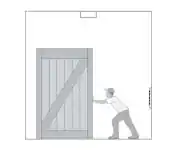
a) Nesse instante, a aceleração é nula e o elevador está descendo
b) Nesse instante, a aceleração é nula e o elevador está subindo
c) Nesse instante, a aceleração vertical do elevador tem sentido para baixo mas não é possível saber se o elevador está subindo ou descendo
d) Nesse instante, a aceleração vertical do elevador tem sentido para cima mas não é possível saber se o elevador está subindo ou descendo
e) Nesse instante, o elevador está descendo e sua aceleração tem sentido contrário ao da velocidade
Ver solução completaQuestão 21
Questão discursiva.
Um bloco de massa está posicionado sobre uma cunha triangular de massa , que faz um ângulo com a horizontal (ver figura abaixo).
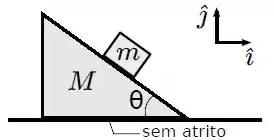
Não há atrito entre a cunha e a superfície horizontal sobre a qual ela se apoia. Considere .
- Se o atrito entre o bloco e a cunha for desprezível, calcule a aceleração horizontal que a cunha deve ter para que o bloco permaneça em repouso em relação à mesma.
- Calcule o módulo da força atuando sobre a cunha que produz a aceleração encontrada no item (a).
- Se , determine a aceleração horizontal mínima da cunha para que o bloco permaneça em repouso em relação à ela.
Considere agora que o coeficiente de atrito estático entre o bloco e a cunha vale .
Questão 22
. A figura ilustra um bloco de massa sobre uma prancha de massa apoiada sobre um piso horizontal perfeitamente liso. Considere o coeficiente de atrito estático entre o bloco e a prancha. Determine o maior valor possível do módulo de que permita movimento solidário dos dois corpos (sem deslizamento relativo) e indique quais são pares ação reação entre o bloco e a prancha.
Questão 23
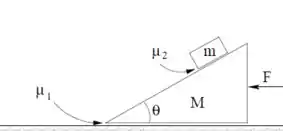
Considere o sistema da figura ao lado. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito cinético entre o bloco de massa M e a superfície do piso é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa m parado sobre o de baixo, se o de baixo estiver parado. Uma força F é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma, que o bloco de cima não deslize sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força F é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a DESCER sobre o de baixo). Dê suas respostas em termos de .
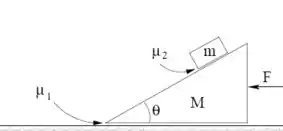
P2.2 – Calcule a aceleração mínima do conjunto.
Ver solução completaQuestão 24
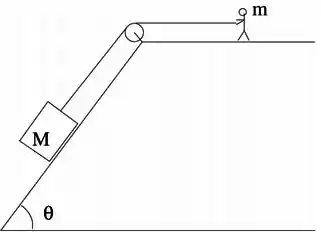
Uma pessoa de massa tenta puxar uma caixa de massa sobre uma superfície inclinada, através de uma corda e uma polia ideais, de acordo com a figura abaixo. A superfície inclinada define um ângulo com a horizontal, e a pessoa encontra-se no topo, em uma superfície horizontal. O coeficiente de atrito estático entre a caixa e a superfície é e o coeficiente de atrito estático entre o sapato da pessoa e a superfície é .
(a) Desenhe na figura todas as forças exercidas na pessoa e na caixa.
(b) Encontre o valor mínimo de para que a pessoa consiga mover a caixa. Verifique seu resultado para o limite para e
(c) Substituindo os valores de , , , e , encontre o mínimo valor de para que seja possível mover a caixa. Utilize a aproximação e .
(d) O que você deverá mudar em seus cálculos se a pessoa também estiver no plano inclinado? Recalcule o resultado do item anterior para este caso.
Questão 25
Dois blocos, e , realizam um movimento retilíneo com aceleração constante. Uma força constante de módulo igual a atua sobre o bloco . O bloco está em repouso em relação ao bloco , lateralmente apoiado a esse como mostra a figura. O coeficiente de atrito estático entre os blocos e vale . Não há atrito entre o bloco e o solo. As massas dos blocos e valem respectivamente, e . Considerando a aceleração da gravidade igual a :
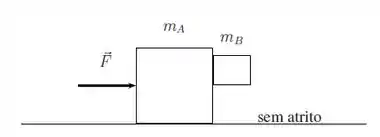
a) Faça o diagrama das forças que atuam sobre cada um dos blocos.
b) Qual o módulo da aceleração dos blocos? Justifique sua resposta.
c) Determine o módulo de todas as forças que atuam sobre o bloco .
d) Qual o menor valor que o módulo da força que atua sobre o bloco deve ter para que o bloco não deslize sobre a superfície do bloco ?
Ver solução completaQuestão 26
Dois objetos e estão presos por cordas a um anel de massa desprezível. O anel também está preso a uma parede por uma terceira corda, que forma um ângulo com a horizontal. Considere que tem massa , e possui coeficientes de atrito estático e dinâmico com a mesa dados por e , respectivamente. Suponha que todas as cordas estão totalmente esticadas.
Dados: . e .
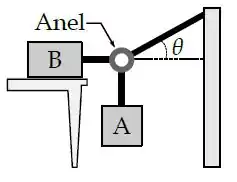
(a) Considerando que o sistema é estático (não se move), faça um diagrama indicando todas as forças que atuam sobre o anel e os objetos e .
(b) Qual o valor da massa para o qual o bloco se encontra na iminência de movimento?
(c) Suponha que . Qual o módulo da tração na corda que conecta o anel a parede?
Ver solução completaQuestão 27
Uma caixa está em repouso sobre a superfície plana na carroceria de um caminhão. O coeficiente de atrito estático entre a caixa e a superfície é . Qual é a aceleração máxima que o caminhão pode desenvolver sem que a caixa deslize da sua carroceria?
Dado:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 28
Uma caixa de massa está sob outra caixa, de massa . Uma pessoa tenta arrastar as caixas, puxando a de cima com uma força de módulo , que faz um ângulo com a horizontal, conforme a figura. Não há atrito entre a caixa debaixo e o solo e os coeficientes de atrito estático e cinético entre as duas caixas são, respectivamente, e . Observa-se que o sistema composto pelas duas caixas se desloca em conjunto para a direita com aceleração de módulo .
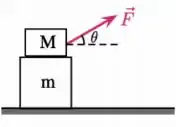
Podemos afirmar que o módulo da força de atrito entre os blocos é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 29
[ENUNCIADO COMUM ÀS QUESTÕES 10 e 11]
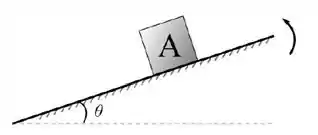
Considere o seguinte experimento para medirmos o coeficiente de atrito estático entre duas superfícies. Colocamos um bloco sobre um plano inclinado cuja inclinação podemos controlar. Inicialmente o plano está na horizontal. Lentamente, aumentamos o ângulo entre o plano e a horizontal, como na figura. Sobre essa situação responda as questões 10 e 11.
[QUESTÃO 10]
Observamos que o bloco começa a se mover quando o ângulo é . Qual dos valores abaixo melhor aproxima o coeficiente de atrito estático entre as superfícies?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 30
Na figura, o fio e a roldana são ideais, e o plano fixo em que se apoia o bloco possui inclinação com a horizontal. Em todas as situações abaixo, o fio permanece tensionado e , mas o bloco pode variar. Quando necessário substituir valores, use .
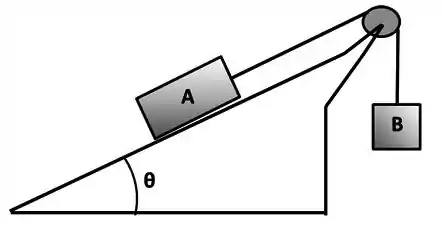
Neste item, . Pendurando-se vários blocos diferentes, descobriu-se que o peso máximo sem que o sistema entre em movimento é . Qual é o peso mínimo de que impede o deslizamento no sentido contrário?
Ver solução completaQuestão 31
10 - Uma caixa com um peso de repousa sobre uma superfície horizontal. Uma pessoa puxa horizontalmente com uma força de e ela não se move. Para iniciar o movimento, uma segunda pessoa puxa verticalmente para cima a caixa. Se o coeficiente de atrito estático for , qual é a menor força vertical para a qual a caixa se move?
A)
B)
C)
D)
E)
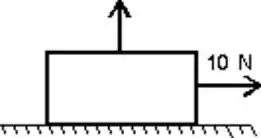
Questão 32
Um bloco de massa está sobre uma mesa horizontal sendo empurrado em movimento retilíneo por uma força constante dada, com velocidade e aceleração de mesmo sentido que a força; o coeficiente de atrito cinético entre o bloco e a mesa é . Sobre esse primeiro bloco há um segundo bloco de mesma massa e rigidamente colado ao primeiro, como indica a figura.
a) Faça um diagrama de forças externas sobre o sistema constituído pelos dois blocos;
b) Calcule o módulo a da aceleração com a qual os blocos se deslocam;
c) Calcule os módulos da força horizontal e da força vertical que o bloco exerce sobre o bloco .
Ver solução completaQuestão 33
Um homem tenta sem sucesso empurrar horizontalmente uma pedra. Podemos afirmar que, nesta situação:
a) o módulo da força de atrito estático é igual à , onde é o coeficiente de atrito estático;
b) o módulo da força aplicada pelo homem na pedra é menor que a força de atrito exercido pelo chão na pedra;
c) se o homem diminuir a força com que empurra a pedra, a força de atrito estática diminui na mesma proporção;
d) o módulo da força de atriro é igual à diferença entre o módulo da força normal e a força que o homem exerce na pedra;
e) nenhuma das anteriores.
Ver solução completaQuestão 34
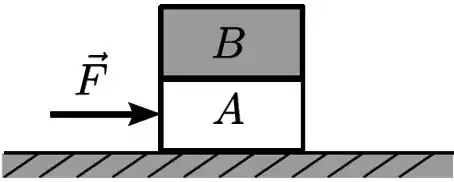
Questão 2) Os blocos e da figura ao lado tem massas e . Considere o fio inextensível, a polia sem atrito e as massas do fio e da polia desprezíveis. Os coeficientes de atrito estático e cinético entre o bloco e a mesa são e , respectivamente.
a) Determine a massa mínima do bloco () para impedir que o bloco deslize. Faça um diagrama de corpo livre para os três blocos.
Ver solução completaQuestão 35
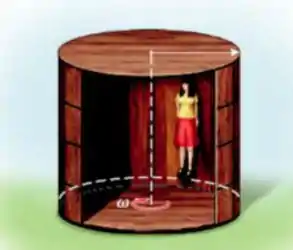
Um brinquedo em um parquet de diversões consiste em um cilindro vertical muito grande que gira sobre seu eixo com velocidade suficiente para que qualquer pessoa dentro do cilindro seja mantida contra a parede quando o chão desaparece. Qual o diagrama corretamente mostra a força agindo sobre a pessoa?
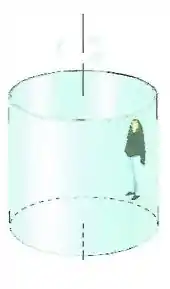
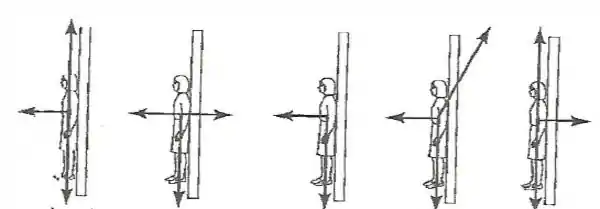
![]()
Questão 36
Q - Um bloco de massa é colocado sobre um bloco de massa , que encontra-se em repouso. Admitindo que os coeficientes de atrito estático e cinético entre os blocos são e , respectivamente, e que os coeficientes de atrito estático e cinético entre o bloco de massa e o solo são e , respectivamente, o
máximo valor de , em Newtons, que pode ser aplicada ao corpo de massa para que o sistema permaneça em repouso é:
Questão 37
Os sapatos de uma enfermeira de massa têm um coeficiente de atrito estático de sobre uma superfície de ladrilho. Os diagramas de corpo livre da enfermeira estão apresentados nos itens abaixo de (a) até (e), onde é a força normal, , força gravitacional e , força de atrito estático. Ao lado do diagram se encontra o valor da aceleração máxima que a enfermeira pode desenvolver. Qual item é verdadeiro se a enfermeira está caminhando para a direita?
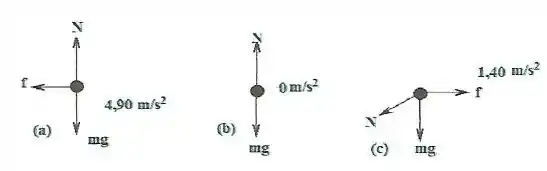
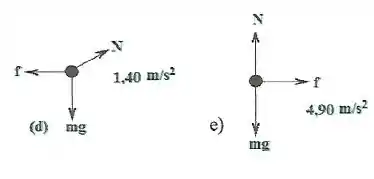
Questão 38
Considere o sistema da figura ao lado. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito cinético entre o bloco de massa M e a superfície do piso é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa m parado sobre o de baixo, se o de baixo estiver parado. Uma força F é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma, que o bloco de cima não deslize sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força F é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a DESCER sobre o de baixo). Dê suas respostas em termos de .
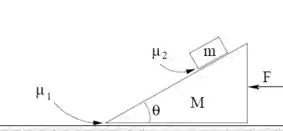
P2.2 – Calcule o valor da normal entre os blocos nessa situação.
Ver solução completaQuestão 39
Um bloco de está sobre outro de que repousa sobre uma mesa lisa (sem atrito). Os coeficientes de atrito estático e cinético entre os blocos são 0,4 e 0,3, respectivamente. Uma força é aplicada ao bloco de paralelamente à superfície da mesa (veja a figura).
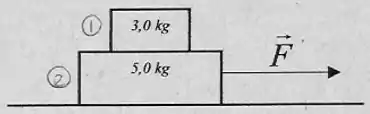
a) Faça um diagrama de forças para cada um dos blocos.
b) Qual é o valor máximo do módulo de que não provoca o escorregamento do bloco de sobre o de ?
c) Calcule a aceleração de cada bloco se for igual a .
Ver solução completaQuestão 40
A figura mostra um brinquedo de levitação em um parque de diversões. O cilindro gira e quando a velocidade angular o chão abaixa e a pessoa fica colada ao cilindro. Qual o diagrama de forças correto?
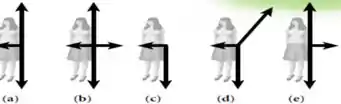
Questão 41
(Cap 6 – Ex 101) Quando uma pequena moeda de é colocada a uma distância de do centro de um prato giratório horizontal que executa três rotações completas em , a moeda não escorrega. Determine (a) a velocidade escalar da moeda, (b) o módulo e (c) o sentido (radialmente para dentro ou para fora) da aceleração da moeda e (d) o módulo e (e) o sentido (para dentro ou para fora) da força de atrito sobre a moeda. A moeda fica na iminência de escorregar quando é colocada a uma distância de do centro. (f) Qual é o coeficiente de atrito estático entre a moeda e o prato giratório?
Ver solução completaQuestão 42
Um bloco encontra-se na iminência de deslizamento sobre um plano inclinado que forma um ângulo com a horizontal. Qual é o valor do coeficiente de atrito estático ?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 43
Uma vagão pode deslizar, sem atrito, sobre uma superfície horizontal. Um bloco , de massa , está encostado na face vertical do bagão, como mostra a figura . O coeficiente de atrito entre o bloco e o vagão é .
Determinar a aceleração mínima do vagão para que o bloco não caia;

Questão 44
Um carro trafega sobre uma estrada horizontal, na forma de um círculo de raio igual a . Sabendo que o coeficiente de atrito estático é , com que velocidade o carro pode trafegar sem risco de derrapar? SE a curva não for horizontal, mas inclinada, achar o ângulo de inclinação para que o carro a possa fazer a curva na ausência de atrito no pavimento.
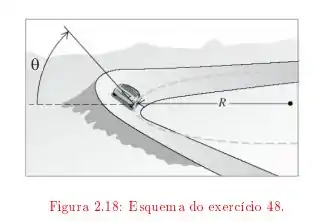
Questão 45
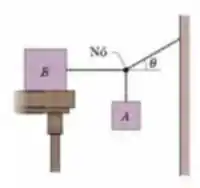
(Cap 6 – Ex 23) O bloco da Fig. 6-31 pesa . O coeficiente de atrito estático entre o bloco e a mesa é ; o ângulo é ; suponha que trecho da corda entre o bloco e o nó é horizontal. Determine o peso máximo do bloco para o qual o sistema permanece em repouso.
Questão 46
Um estudante em um laboratório levanta uma rocha de massa m = 12 kg, e eleva-a, com aceleração desprezível, até a altura D = 1, 8 m, para colocá-la em um armário.
- Qual o trabalho realizado pelo estudante sobre a rocha?
Questão 47
O bloco A da figura abaixo pesa e o bloco B pesa . O coeficiente da força de atrito cinético entre as superfícies dos blocos é . Encontre a magnitude da força horizontal necessária para arrastar o bloco B para a esquerda em velocidade escalar constante
(a) se A repousa em B e se move com ele.
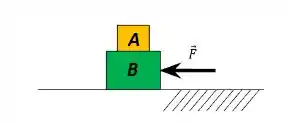
Questão 48
16. Um bloco de madeira está parado sobre uma superfície inclinada num ângulo de graus. Se o bloco fica na iminência de deslizar sobre a superfície, o valor do coeficiente de atrito estático é?
Ver solução completaQuestão 49
Diante de cada afirmação, responda ou corrija aquelas que estiverem errados e justifique com suas palavras o seu raciocínio.
Num jogo de “cabo de guerra”, duas pessoas de mesma massa estão amarradas a uma corda ideal, pela qual se puxam. Vence sempre a pessoa mais forte.
Ver solução completaQuestão 50
Considere o sistema da figura ao lado. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito cinético entre o bloco de massa M e a superfície do piso é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa m parado sobre o de baixo, se o de baixo estiver parado. Uma força F é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma, que o bloco de cima não deslize sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força F é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a DESCER sobre o de baixo). Dê suas respostas em termos de .
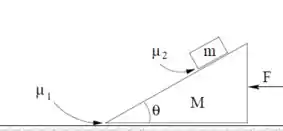
P2.1 – Faça o diagrama de forças nos dois blocos, enquanto há movimento, mas o de cima não se move sobre o de baixo. Marque quais dessas forças são pares de ação e reação. faça outro desenho e separe os blocos para maior clareza.
Ver solução completaQuestão 51
No problema da questão (6), qual é a maior inclinação max da rua para que a carga não deslize na carroceria? Considere ainda que o caminhão se movimente com velocidade constante.
(A) max = arccos(µe)
(B) max = arcsen(µc)
(C) max = arcsen(µe)
(D) max = arctan(µc)
(E) max = arctan(µe)
Ver solução completaQuestão 52
Considere o sistema da figura ao lado. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito cinético entre o bloco de massa M e a superfície do piso é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa m parado sobre o de baixo, se o de baixo estiver parado. Uma força F é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma, que o bloco de cima não deslize sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força F é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a DESCER sobre o de baixo). Dê suas respostas em termos de .
P2.4 – Determine o valor mínimo da força .
Ver solução completaQuestão 53
Uma pessoa tem que deslocar uma caixa de massa M por um plano horizontal com atrito, conforme a figura. Em qual das situações ela fará força maior? Justifique.
Ver solução completaQuestão 54
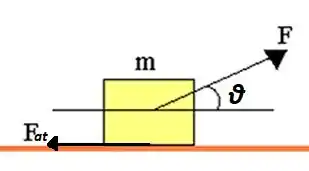
Um bloco de massa está sobre uma mesa horizontal, como mostrado na figura. O bloco é puxado por uma corda sem massa com uma força a um ângulo . O coeficiente de atrito estático . O valor mínimo da força necessária para mover o bloco depende do ângulo . Mostre que
- a expressão para o módulo da força em função do ângulo é dada por .
Questão 55
Um caixote de é arrastado sobre um piso, puxado por uma corda inclinada acima da horizontal. (a) Se o coeficiente de atrito estático é , qual é o valor mínimo do módulo da força para que o caixote comece a se mover? (b) Se , qual é o módulo da aceleração inicial do caixote?
Ver solução completaQuestão 56
Q - A figura ao lado mostra dois blocos em contato, de massas e , que não estão fixados um ao outro. Uma força horizontal age no bloco de massa , como mostra a figura, fazendo com que eles andem juntos sobre uma superfície horizontal sem atrito. Se os coeficientes de atrito estático e cinético entre as superfícies de contato dos dois blocos valem respectivamente e , determine qual é o valor mínimo de necessário (expressado em Newtons) para que não deslize verticalmente em direção ao solo.
Questão 57
Uma caixa de massa é colocada em cima de uma caixa maior de massa como mostrado na figura. Quando uma força de módulo é aplicada na caixa grande, ambas as caixas se movem para a direita com a mesma aceleração. Supondo que o coeficiente de atrito entra as caixas é e que não há atrito entre a caixa maior e o chão, qual é a força atuando na massa menor?
a)
b)
c)
d)
e)
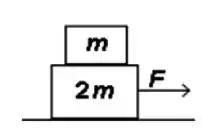
Questão 58
Na figura, um carrinho se movimenta com aceleração em contato com um bloco de massa . O coeficiente de atrito estático entre o bloquinho e o carrinho é . Assinale a alternativa correta:
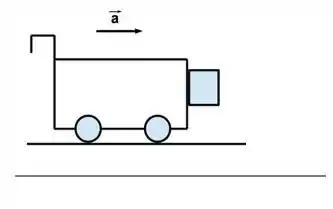
(a) o bloquinho permanecerá em repouso, em relação ao carrinho, para qualquer valor de .
(b) o bloquinho vai cair seja qual for o valor de .
(c) existe um valor de para o qual o bloquinho irá subir.
(d) o bloquinho vai cair se o valor de for menor ou igual a .
(e) existe um valor de acima do qual o bloquinho nunca cai.
Ver solução completa

