Na Fig. 6-15, se a caixa está parada e o ângulo entre a horizontal e a força aumenta, as grandezas a seguir aumentam, diminuem ou permanecem com o mesmo valor: (a) ; (b) ; (c) ; (d) ?
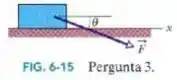
Passo 1
Temos aqui novamente uma questão conceitual, temos que analisar caso a caso. Comecemos com a letra (a).
não é nada mais do que a componente de na horizontal, então:
Como aumenta, diminui e diminui.
Passo 2
Agora, na letra (b), vamos analisar a variação de , que é a força de atrito que a superfície aplica na caixa.
Aprendemos que a nasce quando algum tipo de movimento é incentivado e vai crescendo de acordo com a intensidade da força que gera esse movimento, sempre no sentido oposto. Enquanto não há movimento, tem sempre o mesmo módulo da força horizontal aplicada. Portanto:
Se diminui, diminui.
Passo 3
Já pra letra (c) nos é pedido para avaliar a variação da força normal . Sabemos que o chão não vai furar, portanto, a força normal vai sempre responder com o mesmo módulo e com sentido contrário à componente vertical da força :
Como aumenta, aumenta.
Passo 4
Por último, analisaremos a variação de . Aprendemos que a expressão que rege o módulo da força de atrito máximo é dada por:
Como é constante e aumenta, aumenta.
Resposta
- diminui
- diminui
- aumenta
- aumenta