Questão discursiva.
Um bloco de massa está posicionado sobre uma cunha triangular de massa , que faz um ângulo com a horizontal (ver figura abaixo).
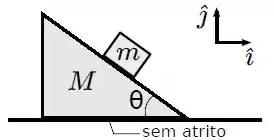
Não há atrito entre a cunha e a superfície horizontal sobre a qual ela se apoia. Considere .
- Se o atrito entre o bloco e a cunha for desprezível, calcule a aceleração horizontal que a cunha deve ter para que o bloco permaneça em repouso em relação à mesma.
- Calcule o módulo da força atuando sobre a cunha que produz a aceleração encontrada no item (a).
- Se , determine a aceleração horizontal mínima da cunha para que o bloco permaneça em repouso em relação à ela.
Considere agora que o coeficiente de atrito estático entre o bloco e a cunha vale .
Passo 1
Letra a)
Para o bloquinho permanecer em repouso com relação à cunha, os dois têm que se mover juntos e a aceleração dos dois tem que ser IGUALZINHA.
As forças que atuam no bloquinho são a força de contato normal e a força peso .
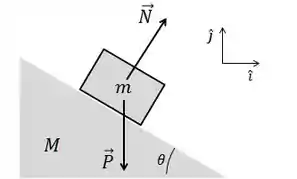
Precisamos escolher os eixos que mais facilitem o problema pra gente, se não caimos num buraco sem fundo! Como a aceleração é horizontal, ao longo do eixo desenhado na figura, então o melhor é usar os eixos da própria figura. Temos então que decompor a força normal:
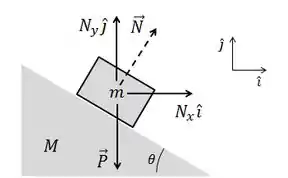
Para achar as componentes em função do módulo da normal , vamos ter que usar um pouquinho de geometria.
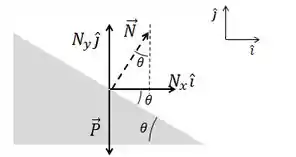
Como a direção é paralela à base da cunha, o ângulo que ela faz com a cunha vai ser também. Além disso, como é normal ao plano da cunha, o ângulo que ele faz com o eixo horizontal é e logo, o ângulo que ele faz com a direção vertical é .
Isso nos diz o seguinte:
Como o bloco não voa do nada, ele não tem aceleração vertical, e assim a força resultante vertical vai ser:
Daí tiramos que:
Enquanto a força horizontal resultante vai ser:
Substituindo o resultado anterior, temos:
Em notação vetorial:
Passo 2
Letra b)
O sistema todo se movimenta junto, com uma aceleração . Podemos então pensar na cunha e no bloquinho juntos, formando um MEGA BLOCO-CUNHA de massa .
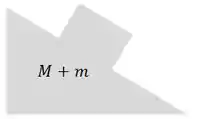
Pela segunda lei de newton, a força necessária pra esse sistema se mover com aceleração é:
Em módulo:
Passo 3
Letra c)
Se considerarmos agora o atrito estático (pois o bloco estará parado em relação à cunha), temos que adicionar essa força no nosso bloquinho lá da letra .
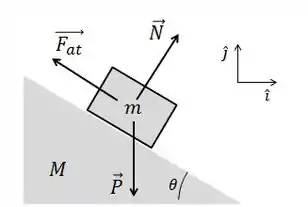
A força de atrito aponta nessa direção pois ele se opõe ao movimento natural do bloquinho escorregar ao longo da cunha. Se o bloco fosse subir pela cunha, o seu sentido seria o contrário.
(Poderíamos considerar que o bloquinho estava prestes a subir, e o atrito estava no sentido oposto, mas esse seria outro problema, pois as acelerações teriam que ser muito grandes).
Assim como decompomos a normal antes, precisamos agora decompor a força de atrito. Porém, como ela tem mesma direção da superfície da cunha, não temos que ficar pensando na geometria da coisa: o ângulo entre e o eixo horizontal é .
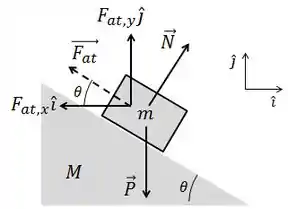
O que nos dá, em módulo:
Fazendo o balanço das forças nos dois eixos, teremos:
Eixo Vertical
Eixo Horizontal
Passo 4
Resumindo as equações que obtivemos no passo anterior:
Vamos tentar agora isolar e para encontrar expressões pra elas com o que é dado no problema.
Da segundo equação:
Substituindo na primeira:
Rearrumando:
Podemos usar isso para achar também uma expressão para a normal:
Agora vamos lembrar sobre força de atrito.
A força de atrito estático vai aumentando até que ela atinja um máximo. Esse máximo é encontrado usando a força normal e o coeficiente de atrito estático.
Substituindo as expressões que encontramos:
Colocando tudo que tem pra direita e tudo que tem pra esquerda, teremos:
Logo, a aceleração mínima é:
Lembrando que estamos considerando que o que faz com que . Isso se dá porque, neste caso, se a cunha estivesse parada, o bloquinho iria deslizar ao longo dela.
Duas observações:
- Se tivéssemos , a aceleração mínima seria zero. Isso é porque nós recaímos no caso de encontrar o ângulo limite da cunha para o qual o bloco não desliza, com a cunha parada.
- Se mudássemos o sentido da força de atrito (para fazer isso, basta multiplicar a expressão que obtivemos por ) nós encontraríamos um valor máximo para a aceleração. Isso significa que pra acelerações maiores que ela o bloco iria deslizar para cima.
Resposta
Letra a)
Letra b)
Letra c)