UFMG – Cálculo 2 – P2 – Questão 3
Considere a curva em coordenadas polares, dada por
- Faça um esboço da curva
- Encontre a área que ela delimita no 1º quadrante
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou facilitar para você! O problema nos deu uma curva em coordenadas polares:
E pediu duas coisas: um esboço dessa curva e a área que ela delimita no primeiro quadrante.
Para esboçar essa curva, é interessante que a gente saiba alguns pontos chave: valores de para alguns ângulos. Eu sugeriria alguns:
Encontrando os valores de nesses pontos, teremos como a curva se comporta em cima dos eixos ordenados e na metade dos quatro quadrantes .
Com esses valores na mão, é só jogar o gráfico e unir os pontos! Lembrando que o seno tem característica de ser uma função suave, então aqui não tem bicos!
Na segunda parte, determinar a área é partir para a integração! Lembrando que o diferencial de área em coordenadas polares é , aplicar os limites apropriados!
O varia entre e a expressão dada e o primeiro quadrante nos diz que .
Beleza?
Mas calma, vou fazer passo a passo com você! Vamos lá?
Passo 2
Letra (a):
Para fazer o esboço, vamos calcular os valores de correspondentes com os ângulos que comentei com você lá no passo anterior!
A curva dada foi:
Os valores de que vamos calcular são:
Então, vamos começar?
Para :
Para :
Para :
Esses foram os principais pontos do primeiro quadrante. Vamos para o segundo quadrante?
Para :
Para :
Agora para o terceiro:
Para :
E para :
E por fim, para o quarto:
Para :
E em temos o mesmo valor que em :
Ufa! Conseguimos calcular todos esses pontos!
o próximo passo é reunir todos esses dados e esboçar essa curva!
Passo 3
Os valores que calculamos são:
E agora vamos reunir esses pontos em um esboço:
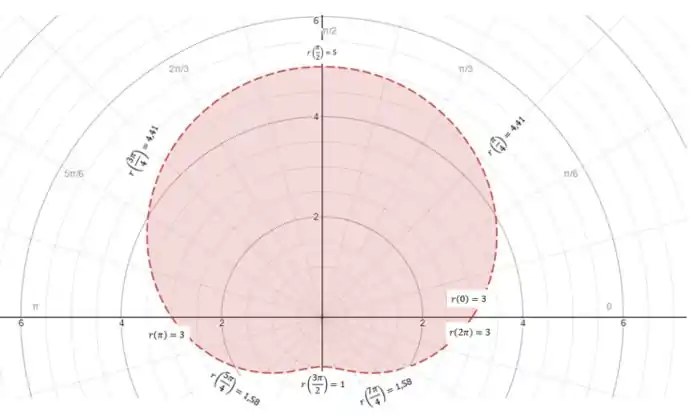
Olha que bonitinha! Está aí nossa curva!
Vamos para a letra (b)?
Passo 4
Letra (b):
Agora o problema pede para calcularmos a área que essa curva compreende no primeiro quadrante.
Bom, como estamos falando em coordenadas polares, precisamos usar o diferencial de área em polares:
A área no primeiro quadrante tem ! E o ? Bom, como vemos na figura, varia de até a curva mesmo. Então os limites de integração são:
Assim a área que precisamos calcular é:
Substituindo os limites de integração temos:
Certo? #partiuintegrar
Passo 5
Agora vem a parte braçal: integrar essa área!
Vamos começar com a integral de dentro, em :
Beleza?
Mas , então:
Agora que temos o integrando de forma mais simplificada (e sem nenhum , o que é muito importante!) vamos substituir isso na integração em !
Passo 6
A área que precisamos calcular era:
Resolvemos a integral de dentro, agora vamos para a de fora:
Beleza? E por fim precisamos aplicar os limites:
Ufa! Terminamos! Aqui está a área que essa curva delimita no primeiro quadrante!
Tranquilo?
Bora pra próxima?
