[UFABC] Cálculo 1 - Lista de Exercícios 7
Calcule a partir da definição as seguintes integrais:
c)
Passo 1
Fala aí, gente bonita! Essa questão é uma continuação do que estamos aprendendo, aumentamos um degrauzinho da dificuldade, mas vamos usar a mesma definição:
Nesse intervalo de integração da função já temos alguns valores:
Podemos dividir esse intervalo em partes, então teremos que cada pequena partição será:
Ficamos com:
E olhando para dentro do nosso somatório, precisamos definir quais são os valores de :
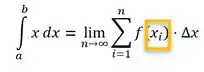
E vamos calcular cada um dos valores de da seguinte forma:
Logo substituindo os nossos valores:
Agora pensando na função , podemos pegar a função que está sendo utilizada dentro da integral:
E substituindo o valor de que acabamos que calcular:
Ótimo, parabéns por chegar até aqui, agora é hora de voltarmos ao somatório com todo esse grupo de informações que levantamos:
Substituindo nossos valores:
Passo 2
Vamos resolver esse limite para igualar a integral:
Vamos começar jogando tudo que não depende de para fora do somatório:
Agora vamos relembrar a seguinte relação do somatório, presta bastante atenção, porque é a dica de ouro:
Então substituindo esse somatório dentro de nosso limite, temos:
Simplificando os valores que estão no numerador com o valor que está no denominador:
Fica tranquilo e joga essa parcela pra fora do limite:
Realizando esse limite maravilhoso, chegamos ao resultado igual a:
Substituindo em nossa conta:
Nossa integral inicial é igual a:
Resposta
c)