Para a função dada abaixo, esboce seu gráfico e em seguida calcule .
Passo 1
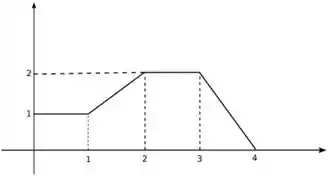
O esboço do gráfico de pode parecer difícil porque a função é dividida em muitas partes, mas na verdade é bem tranquilo, veja só:
O mais importante é dividir o eixo nos intervalos dados pra saber até onde cada parte da função vai
![]()
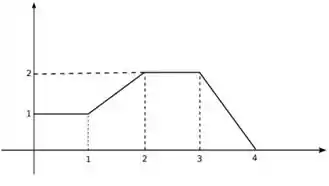
Observe que quando a função se torna ela é um reta crescente e quando se torna ela é uma reta decrescente com zero da função em . Portanto, esboçando o gráfico teremos o seguinte:
Passo 2
Agora vamos montar a integral pedida e calcular. Observe que o intervalo de integração é de a . Como a função muda de lei de formação dentro desse intervalo, teremos que dividir a integral. Os intervalos em que a função está dividida são
Entao, temos que fazer uma integral para cada intervalo desses, assim. Assim, de até que é o primeiro intervalo, a integral fica:
Para cada um dos intervalos então teremos a integral total de até :
Substituindo pela lei de formação de cada intervalo e calculamos as integrais:
Resposta