Se
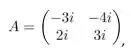
então é:
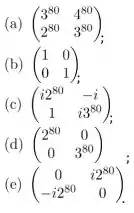
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é descobrir o valor de . Bem, fica aqui a dica, se temos que fazer uma potência muito alta de uma matriz, então muito provavelmente teremos que diagonalizar a matriz. Isto é escrever na forma . Então vamos resolver essa questão!!!!

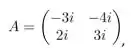
vamos calcular seus autovalores. Por definição, eles são as raízes do polinômio
E suas raízes são
Passo 2
Agora que temos os nossos autovalores, podemos calcular (vc acha que temos que pegar os autovetores, né? Mas se liga só) 😉
como os autovalores são
A matriz é:
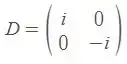
Então:
Mas é:
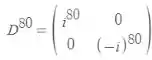
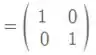
então
Ou seja, é a matriz identidade. Legal, né? Essa matriz está presente na alternativa

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊