Calcular , sabendo que são vértices de um triângulo de área .
Passo 1
Esse exercício é meio que o inverso do anterior, pois é nos dado os pontos que formam o triângulo e também é nos dada a área do triângulo. Então, o que devemos descobrir é a coordenada do ponto para que o triângulo tenha área .
Sabemos que o módulo do produto vetorial entre os vetores nos dará a área do paralelogramo, e que a área do paralelogramo é duas vezes a do triangulo, então temos que:
Passo 2
Sabendo a área do paralelogramo, sabemos quanto deve dar o módulo do produto vetorial entre . Então, vamos calcular o produto vetorial, mas primeiro vamos achar os vetores que precisamos.
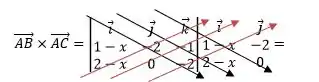
Passo 3
Já temos o produto vetorial. Agora, é calcular o módulo e igualar com a área do paralelogramo que já descobrimos quanto vale:
Resolvendo a igualdade acima, temos:
Resolvendo a equação de 2º grau chegamos em duas soluções: