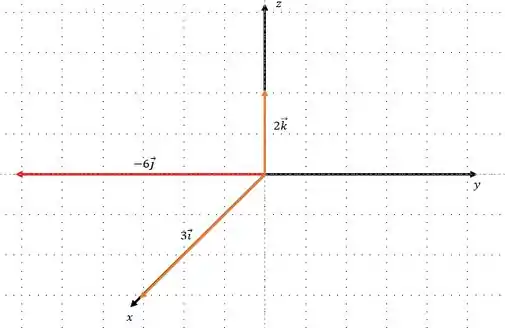
Mostrar num gráfico um representante de cada um dos seguintes vetores:
Passo 1
São nos dados vetores na base cartesiana. E pede para que representemos num gráfico. Para cada um teremos que calcular o produto vetorial entre os vetores dados e depois desenhar num gráfico. Temos duas formas de fazer isso. Em cada item será apresentada uma forma.
Passo 2
- Primeira maneira de se resolver: Maneira analítica
No item nos é dado . Pode parecer uma representação esquisita, mas ela está na base cartesiana, ou seja:
- indica a coordenada .
- indica a coordenada .
- indica a coordenada
Assim, é nos dado o seguinte produto vetorial:
Agora que sabemos a representação mais comum a nós, vamos fazer o produto vetorial:
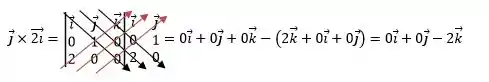
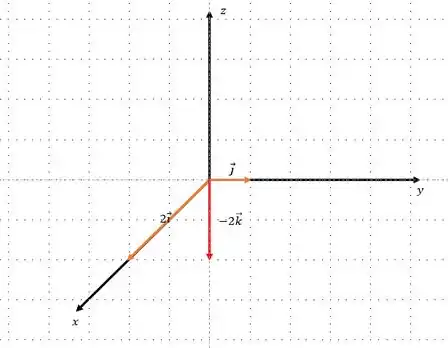
Passo 3
Agora que já sabemos interpretar a representação cartesiana, fica mais tranquilo identificarmos os vetores .
Se dominamos a regra da mão direita e a base cartesiana, esse jeito pode ser mais rápido.
Bom, primeiro, sabemos que os versores da base cartesiana são ortogonais entre si, então, pela regra da mão direita sabemos que:
A direção e o sentido do nosso produto vetorial nós já achamos, simplemente aplicando a regra da mão direita. Mas, qual o módulo?
Bom, sabemos que:
Como sabemos, o Ângulo entre e é , assim temos que:
Então,