Exercícios de Produto Vetorial - Lista de Exercícios Resolvida

Determinar o valor de para que o vetor seja simultaneamente ortogonal aos vetores e .

Mostrar num gráfico um representante de cada um dos seguintes vetores:

Calcular a área do triângulo de vértices

Sabendo que e é o ângulo entre e , calcular .

Calcule sendo (referidos a uma base ortonormal positiva ).

Dados os vetores , calcular a área do paralelogramo determinado pelos vetores .

Calcular , sabendo que são vértices de um triângulo de área .

Prove que se e então ou . Interprete geometricamente.

Sejam os vetores . Calcular o valor de para que a área do paralelogramo determinado por seja igual a .

Determinar um vetor unitário simultaneamente ortogonal aos vetores e . Nas mesmas condições, determine um vetor de módulo 5.

Se são vértices de um tetraedro de , então sua altura relativa à base ABC mede:

Seja um triângulo de área . Sejam , e pontos tais que , e . Calcule a área do triângulo .

Assinale a área do paralelogramo definido pelos pontos , , e :

a)

b)

c)

d)

e) Não sei

Considere o prisma triangular reto (isto é, suas bases são triângulos e suas faces laterais retângulos) de vértices

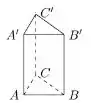
Sabe-se que e o volume do prisma é igual a . Se a primeira coordenada de é positiva ela é:

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.

(d) Se e então a área do paralelogramo formado por e é igual a seja qual for o valor de.

(e) Se e são vetores não nulos de e tais que , então .

Considere os pontos

e os vetores:

(d) Determine pontos diferentes e tais que os pontos:

• A, B, C e determinem um paralelogramo
• A, B, C e determinem um paralelogramo
• A, B, C e determinem um paralelogramo

(e) Determine as áreas destes três paralelogramos.

Seja o plano que contém a reta de equação

E o ponto . Se uma equação geral de é

Então vale

Considere os vetores de

b) Determine, se possível, um vetor tal que

a) Determine um ponto para que os pontos

e determinem um paralelogramo de . Calcule a área do paralelogramo .

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmativa for falsa, exiba um contraexemplo.

c) Se e são vetores não nulos e com a mesma direção, então

d) Se e são vetores do ortogonais e de mesmo módulo, então

Considere que em relação a uma base ortonormal e .

1. Determine a área do triângulo .
2. Determine a altura relativa ao lado do triângulo .

Seja um conjunto linearmente independente de três vetores em , e seja um ponto qualquer em . Considere os pontos , e . Então a área do triângulo de vértices é igual a:

Sejam e vetores quaisquer. Seja . Mostre que .

Considere as seguintes afirmações:

para quaisquer e quaisquer , vale que:

para quaisquer , vale que:

para quaisquer , vale que:

Assinale a alternativa correta:

apenas as afirmações e são verdadeiras

apenas a afirmação é verdadeira

apenas a afirmação é verdadeira

apenas as afirmações e são verdadeiras

apenas a afirmação é verdadeira

Dados os pontos , e , vértices de um triângulo. Determine o comprimento da altura relativa ao vértice e calcule a área do triângulo .

Se são tais que é a solução do sistema

Então o produto é igual a

a) 6

b) -24

c) 36

d) -8

e) 12

Considere fixada uma orientação de e seja uma base positiva de tal que e tal que seja ortogonal a e a . Suponha que , e que a medida do ângulo entre e seja igual a . Temos que é igual a:

a)

b)

c)

d)

e)

Considere os vetores de

c) Determine, se possível, um vetor cujo módulo seja e que seja perpendicular aos vetores e (isto é, ).