Considere os pontos
e os vetores:
(d) Determine pontos diferentes e tais que os pontos:
- A, B, C e determinem um paralelogramo
- A, B, C e determinem um paralelogramo
- A, B, C e determinem um paralelogramo
(e) Determine as áreas destes três paralelogramos.
Passo 1
(d) Vamos esquematizar o que tá acontecendo em cada item dessa questão.
Vamos considerar os pontos genéricos O, P, Q e R.
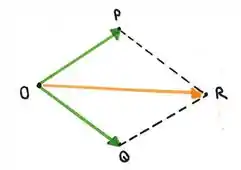
Se montamos os vetores , e , vamos ter, pela regrinha de soma de vetores:
Mas
Então conseguimos escrever o ponto R como:
No caso do paralelogramo formado pelos pontos A, B, C e , vamos ter o ponto e os vetores:
Substituindo na relação genérica que achamos antes:
Mas podemos também fixar o ponto e encontrar os vetores:
Substituindo na relação, vamos achar outro ponto:
Por último, poderíamos ter fixado o ponto Aí teríamos os vetores:
Com isso, achamos o último ponto:
Passo 2
(e) Se temos dois vetores e , podemos formar um paralelogramo traçando vetores paralelos a eles:

Nesse caso, a área do paralelogramo vai ser dada por
Vamos fazer isso pra cada paralelogramo que achamos no item anterior.
Para o paralelogramo
Para o paralelogramo
Para o paralelogramo
Resposta
(d)
(e) , e