Determinar o valor de para que o vetor seja simultaneamente ortogonal aos vetores e .
Passo 1
O problema nos fornece os seguintes dados:
Dados:
Com esses dados, o exercício pede para determinarmos o valor de para que o vetor seja ortogonal (forme ) simultaneamente aos vetores e .
Buguei na parte que fala “simultaneamente ortogonal”!!!

Vamos relembrar um detalhe que vai nos ajudar ;).
Passo 2
Na teoria vimos algumas propriedades do produto vetorial! Lembra? Pois é, eu sei que eram muitos, mas uma delas vai nos ajudar muito. Essa aqui!
![]()
Matou a charada?
Então, sabemos que o produto vetorial gera um vetor, e ainda a propriedade nos diz que esse vetor é simultaneamente ortogonal aos dois vetores que o formam. É tudo o que precisamos. Então, para acharmos , precisamos forçar que ou também que , no caso iremos obter vetores oposto.
Passo 3
Então agora é mão na massa!!!
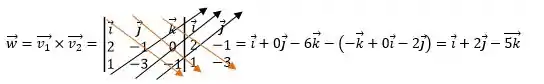
Se você fizer , chegarás em:
Nesse caso, a conta só vai fazer sentido com , pois em e igualando a , teremos: