Unb cálculo 1 lista lista de aplicação - cálculo 1 lista 4
Duas partíıculas carregadas com cargas de módulos 
interagem com uma força
eletrostática. Segundo a Lei de Coulomb, o módulo dessa força, em Newtons, é modelado
pela função
dada por
, onde 
e resolva os itens a seguir.
(a) Encontre 
(dez milhões de Newtons).
(b) Encontre 
(um milionésimo de Newton).
(c) Determine 
.
(d) Faça um esboço do gráfico de 
.
Passo 1
Fala pessoal, tudo bem com vocês? Vamos para mais uma questão de cálculo 1. Primeiramente, quais informações são passadas no enunciado?
Temos que nossa função $F$ é dada por:
,mas é informado que 
pode ser escrita como:
Passo 2
Vamos começar resolvendo a letra a)
nela, queremos saber qual valor de 
E aí? Como vamos descobrir que valor é esse? O que vocês acham?
Primeiro, vamos descobrir para que valor de 
Então temos que:
então
logo:
invertendo
tirando a raiz
Bem, sabemos que quando 
Passo 3
Agora podemos fazer a letra b). Podemos observar que essa letra é parecida com a letra a). Pois queremos obter 
.
Vamos fazer essa questão da mesma forma que fizemos a letra a). Primeiro vamos obter 
então
logo:
invertendo
tirando a raiz
Bem, sabemos que quando 
Passo 4
Já fizemos metade da questão.
Vamos partir para a letra c). Dessa vez, queremos os limites no infinito da função de força. Ou seja, queremos entender o comportamento assintótico da função quando 
. Vamos começar pela primeira.
Como nossa função 
Sempre que aumentamos 
será bem próxima de zero. Logo:
De forma oposta, sempre que diminuímos 
será bem grande. Logo:
Passo 5
Para finalizar a questão, vamos fazer um esboço de 
, e que
Então nossa função tem a forma:
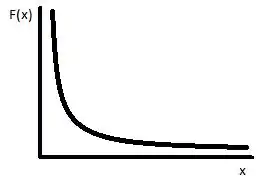
Prontinho pessoal. Com isso terminamos mais uma questão de Calculo 1, espero que os passos tenham ficado claros. Até a próxima!! :)
Resposta
Ei, a resposta está no passo a passo :)