12) Seja a superfície cônica de vértice , , de base situada no plano com raio e com componente não negativa. Seja
Sendo de classe em . Calcule o fluxo de através de .
Passo 1
Se o problema nos pediu fluxo de sobre uma superfície , com toda certeza o que ele está buscando é que façamos uma integral de superfície:
Para resolver essa integral, poderíamos seguir basicamente 2 caminhos:
1º - Fazer de uma forma direta (parametrizando e tudo mais)
2º - Aplicar o Teorema de Gauss.
Pow, perceba que nem temos muitas informações sobre o Campo para calcular pelo método direto, afinal não temos informações sobre .
Então vamos tentar pegar o caminho alternativo, o seja por , mas será que o divergente de ajuda a eliminar essas derivadas parciais de aí?
Calculando as derivadas parciais:
Então...
Pow! Como o é de , então, podemos afirmar que...
Pow, com um divergente simples e convidativo (se parece com a equação da esfera) sim, o problema está pedindo que façamos por Gauss!
Passo 2
O teorema basicamente é a igualdade maravilhosa:
Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:
1º - Uma superfície fechada delimitando o sólido :
2º - Sem singularidades na função Vetorial:
3º - Superfície orientada positivamente:
Vem comigo averiguar essas condições ;D
Passo 3
1º - Uma superfície fechada delimitando o sólido :
Se desenharmos a superfície que queremos o fluxo, como o problema nos sugeriu,
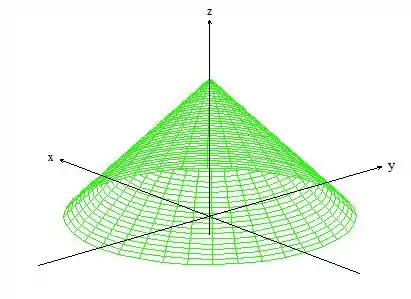
Veja que ela nos representa um cone da boca pra baixo e com o vértice em . Infelizmente ela é uma superfície aberta, logo, para aplicar o Teorema teremos que fecha-la. Podemos fazer isso com o plano ...
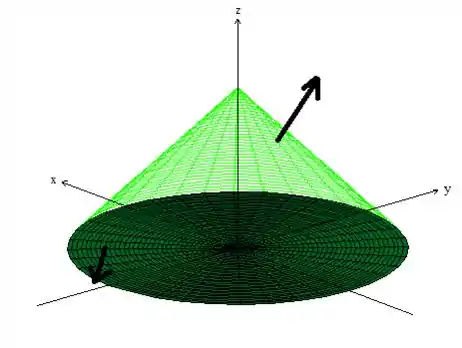
Veja então que o sólido onde devemos integrar agora é fechado pelas superfícies e por esse circulo de raio que vamos chamar de , logo...
Como queremos o fluxo só em , isolemos...
Passo 4
2º - Sem singularidades na função Vetorial:
Esse campo Vetorial funciona em todas as situações já que as derivadas são de classe e a coordenada não tem nenhum bug como uma divisão por ou algo do tipo.
3º - Superfície orientada positivamente:
Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado, afinal o vetor tem a componente positiva...
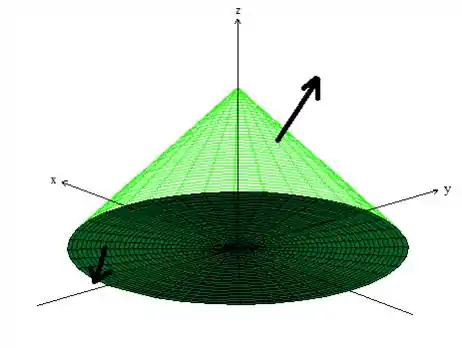
(Observe que para tudo estar orientado positivamente, precisamos de um vetor apontado pra baixo)
Passo 5
Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...
Então vamos lá, e começando com a integral tripla...
vezes a integral de representa...
Como é um cone de altura e a base é uma circunferência de raio , então...
Passo 6
Para a integral de superfície em cima do círculo no plano ...
Veja que o vetorsinho normal a esse cara é...
Logo...
O dessa superfície é já que o círculo está no plano ...
A integral de é a área de , ou seja, a área do disco de raio como calculamos ali em cima...
Passo 7
Voltando para a integral de superfície que queremos...
E substituindo tudo...