Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Superfície Aberta

Ver Teoria
Exercício 1112345678910121314151617181920212223242526272829303132333435363738394041424344454647

Enunciado

8) Seja F → x ,   y ,   z = z   a r c t a n   y 2   i → + z 3   l n   x 2 + 1   j → + z k → . Determine o fluxo de F → através da parte do parabolóide x 2 + y 2 + z = 2 que está acima do plano z = 1 , sendo n → a normal com a componente z não negativa.

Passo 1

Se o problema nos pediu fluxo de F → sobre uma superfície S , com toda certeza o que ele está buscando é que façamos uma integral de superfície:

∬ S   F → ⋅ d S →

Para resolver essa integral, poderíamos seguir basicamente 2 caminhos:

1º - Fazer de uma forma direta (parametrizando e tudo mais)

2º - Aplicar o Teorema de Gauss.

Veja você que o campo é um pouco complicado para se fazer uma integral de superfície direto com ele. Além disso, se você quer mais certeza ainda que de fato vamos resolver o problema pelo Teorema de Gauss, calcule o divergente...

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 2 ∂ z

Como

F → x ,   y ,   z = z   a r c t a n   y 2   i → + z 3   l n   x 2 + 1   j → + z k →

Calculando as derivadas parciais:

1 )                       ∂ F 1 ∂ x = ∂ z   a r c t a n   y 2   ∂ x = 0

2 )                 ∂ F 2 ∂ y = ∂ z 3   l n   x 2 + 1   ∂ y = 0

3 )                                                                 ∂ F 2 ∂ z = ∂ z ∂ z = 1

Logo...

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 2 ∂ z = 1

Pow, com um divergente simples e convidativo, sim, o problema está pedindo que façamos por Gauss!

Passo 2

O teorema basicamente é a igualdade maravilhosa:

∬ ∂ W   F → ⋅ d S → = ∭ W   d i v   F →   d V

Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:

1º - Uma superfície fechada ∂ W delimitando o sólido W :

2º - Sem singularidades na função Vetorial:

3º - Superfície orientada positivamente:

Vem comigo averiguar essas condições ;D

Passo 3

1º - Uma superfície fechada ∂ W delimitando o sólido W :

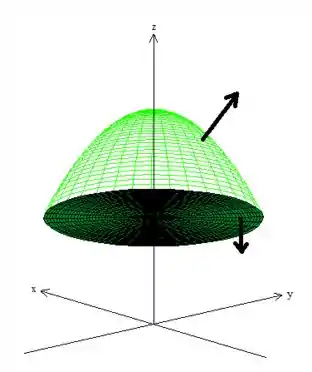
Se desenharmos a superfície S que queremos o fluxo, como o problema nos sugeriu,

x 2 + y 2 + z = 2       →               z = 2 - x 2 - y 2

Veja que ela nos representa um parabolóide que termina com a boca pra baixo. Como queremos apenas a parte com z ≥ 1 ...

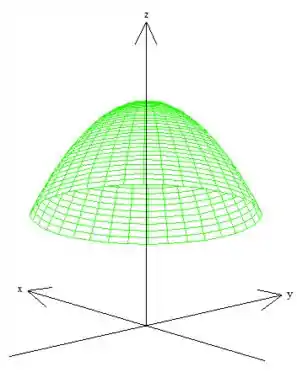
Infelizmente ela é uma superfície aberta, logo, para aplicar o Teorema teremos que fechá-la. Podemos fazer isso com o plano z = 1 ...

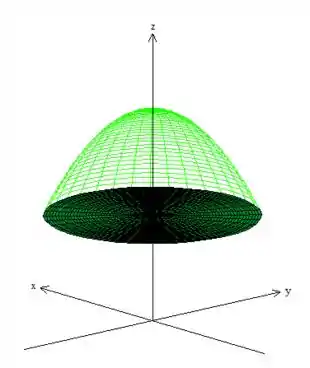
Veja então que o sólido W onde devemos integrar agora é fechado pelas superfícies S e por esse plano que vamos chamar de S 2 , logo...

∬ ∂ W   F → ⋅ d S → = ∭ W   d i v   F →   d V       →

∬ S   F → ⋅ d S → + ∬ S 2   F → ⋅ d S → = ∭ W   d i v   F →   d V   →

Como queremos o fluxo só em S , isolemos...

∬ S   F → ⋅ d S → = ∭ W   d i v   F →   d V - ∬ S 2   F → ⋅ d S →

Passo 4

2º - Sem singularidades na função Vetorial:

F → x ,   y ,   z = z   a r c t a n   y 2   i → + z 3   l n   x 2 + 1   j → + z k →

Esse campo Vetorial funciona em todas as situações, afinal ele não tem nenhuma divisão por 0 ou algo do tipo.

3º - Superfície orientada positivamente:

Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado, afinal o vetor n → tem a componente z positiva...

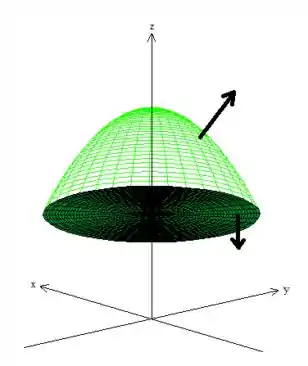
Passo 5

Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...

∬ S   F → ⋅ d S → = ∭ W   d i v   F →   d V - ∬ S 2   F → ⋅ d S →

Então se queremos a integral de superfície S , calculemos a integral tripla e essa integral de superfície em cima de S 2 . Eu sei... Parece insano isso neh? Trocando uma integral para resolver duas... Mas cara, acredite em mim, essa é a maneira mais rápida que temos 😐!

Passo 6

Então vamos lá, e começando com a integral tripla...

∭ W   d i v   F →   d V = ∭ W   1   d V

Essa integral tripla que gerou é igual ao volume de W . Porém o sólido está dentro de um parabolóide, ou seja, essa informação pra gente não serve de muita coisa, neh? Então vamos resolver na marra mesmo, ou seja, primeiro descrever a região:

Descrevendo W :

Como estamos falando de um pedaço de um parabolóide, podemos utilizar as mudanças para coordenadas cilíndricas:

x = r   c o s   θ  

y = r   s i n   θ  

z = z

Onde o Jacobiano dessa mudança é:

J = r

E uma equação que nos ajuda muito é a equação do cilindro:

x 2 + y 2 = r 2

Passo 7

Bem, não devemos sair de uma mudança de coordenadas sem antes dizer onde os parâmetros variam:

Para encontrar a variação de r e θ , devemos olhar pra projeção do sólido no plano x y ...

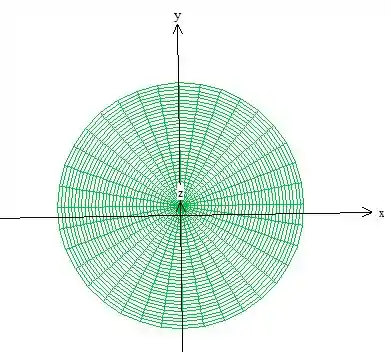
Veja que essa projeção se parece muito pelo método gráfico com um círculo. Não podemos ficar no “se parece” neh? Devemos ter certeza, por isso vamos encontrar a equação dessa projeção.

Observe que ela é o encontro da equação do plano z = 1 com a equação do paraboloide: z = 2 - x 2 - y 2

1 = 2 - x 2 - y 2     →

x 2 + y 2 = 1

Veja que a intersecção de fato é uma circunferência de raio 1 , onde podemos concluir que o Raio r ...

0 ≤ r ≤ 1

E o ângulo θ ...

0 ≤ θ ≤ 2 π

Já variação do z , bem ele é o cara que varia de cima pra baixo no sólido:

Ou seja...

P l a n o   z = 1 ≤ z ≤ p a r a b o l ó i d e →

1 ≤ z ≤ 2 - x 2 + y 2 →

Agora, se estamos em coordenadas polares...

1 ≤ z ≤ 2 - r 2

Passo 8

Voltando então para a integral que devemos resolver:

∭ W   d V = ∭ W     d V =

Substituindo tudo...

∭ W     d V = ∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2 J   d z d r d θ =

∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2 r   d z d r d θ =

Calculando a integral de dentro...

∫ 0 2 π ∫ 0 1 ∫ 1 2 - r 2   d z r d r d θ = ∫ 0 2 π ∫ 0 1 r 1 - r 2 d r d θ =

∫ 0 2 π ∫ 0 1 r - r 3 d r d θ =

Agora a do meio...

∫ 0 2 π ∫ 0 1 r - r 3 d r d θ = ∫ 0 2 π r 2 2 - r 4 4 0 1 d θ =

1 2 2 - 1 4 4 ∫ 0 2 π d θ = π 2

Passo 9

Vamos calcular agora a integral de superfície em S 2 ...

∬ S 2   F → ⋅ n →   d S

S 2 foi a superfície que adicionamos para tampar o buraco, ou seja é o plano z = 1 ...

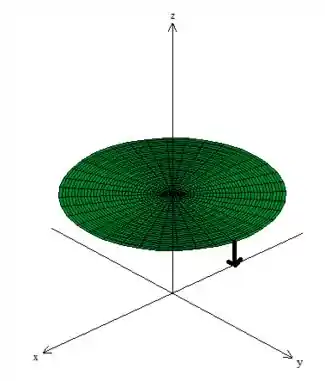
Essa superfície tem o vetorzinho normal n → apontado para baixo e ele é unitário, então...

n → = 0 ,   0 ,   - 1

Logo...

F → ⋅ n → =

z   a r c t a n   y 2   ,   z 3   l n   x 2 + 1   ,   z ⋅ 0 ,   0 , -   1 =

- z

Como no plano o z é 1 , então...

F → ⋅ n → = - 1

Substituindo na integral de superfície...

∬ S 2   F → ⋅ n →   d S = - ∬ S 2     d S

Bem, a integral virou o negativo da área de S 2 . Ora bolas, S 2 não é uma circunferência de raio 1 ?...

∬ S 2   F → ⋅ n →   d S = - π 1 2 = - π

Passo 10

Regressando a integral do problema...

∬ S   F → ⋅ d S → = ∭ W   d i v   F →   d V - ∬ S 2   F → ⋅ d S → →

∬ S   F → ⋅ d S → = 1 2 π - - π →

∬ S   F → ⋅ d S → = 3 π 2

Resposta

3 2 π