Seja a porção da esfera:

Compreendida entre os planos e , com . Calcular:

Onde é a normal unitária a cuja terceira coordenada é sempre positiva e é definido por:

Substituindo na fórmula:

Agora precisamos enxergar nossa região . Fazendo um corte da esfera em , obtemos um círculo de raio e a reta .

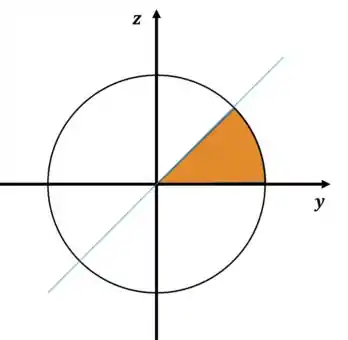
Podemos ver que a região em questão é um oitavo da esfera, portanto:

Agora precisamos separar a integral da região para calcularmos o fluxo que queremos. Temos que, como:

É válida a relação:

Como o que é pedido pelo enunciado é o fluxo pela porção da esfera, então vamos calcular os outros dois e isolar este. Vamos encontrar os conjuntos que representam os planos. Temos que para o primeiro:

Substituindo na equação da esfera, temos a fronteira da região:

Portanto, aliado ao fato de que , temos o conjunto do primeiro plano:

Que é um semicírculo no plano né? Então dá pra gente ver que a normal dele vai estar na direção ! E com o sentido pra termos orientada do jeito que ele pede no enunciado:

Então:

Note que as componentes e do campo vetorial não importam pois o vetor normal as zeraria.

Fazendo a mesma lógica para o segundo plano, temos que:

Substituindo na equação da esfera, temos a fronteira da região:

Logo, podemos parametrizar o segundo plano de forma explícita como abaixo

Então, os vetores normais serão do tipo

Pode conferir que ele aponta para fora do sólido, conforme exigido no enunciado:

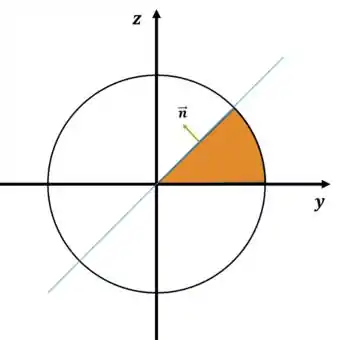
Por fim fazemos a maldita conta, não esquecendo de substituir a condição :

Que segue:

E agora nos resta uma conta chata em coordenadas polares.

Agora para fazer a integral dupla, vamos passar para coordenadas polares

De onde tiramos o novo domínio em coordenadas polares:

Substituindo tudo, junto com o domínio e etc:

Agora é papo de fazer conta:

Logo, temos que:

Basta substituir todos os valores:

Isolando:

Voilá! Chato. Mas faz parte, né...