Teorema de Gauss, Integrais de superfície - caso vetorial
Seja um campo vetorial em .
Seja a superfície parametrizada por
e orientada de forma que o vetor normal possua terceira componente não positiva.
Use o Teorema de Gauss para calcular o fluxo do campo vetorial através da superfície .
Passo 1
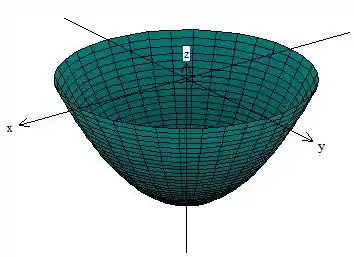
O gráfico da função é alguma coisa desse tipo aqui
O Teorema de Gauss nos diz que
Ele calcula o fluxo do campo vetorial através de uma superfície fechada. Po, mas a nossa superfície não é fechada, então como vamos fazer?!
O que temos que fazer é fechar a nossa superfície com, por exemplo, um disco circular de raio 1 no plano .
Fazendo isso, vamos ter uma superfície fechada onde podemos aplicar o Teorema de Gauss. Lembra qual a restrição desse teorema? A normal deve estar apontando para fora do sólido!
Note que o enunciado ta dizendo que a normal possui componente negativa (não positiva), ou seja, está para baixo e portanto para fora do sólido mesmo =D
Show! Vou chamar a superfície em que queremos calcular o fluxo de e a nossa “tampa” de .
Ah! É importante ficar ligado que, para fechar a superfície e aplicar o Teorema de Gauss é mais jogo você quebrar um pouco a cabeça pra encontrar uma superfície relativamente simples, como nós fizemos.
Beleza, agora podemos seguir com a nossa vida.
Passo 2
Vamos começar calculando
Beleza? O divergente de é dado por:
Passo 3
Como se trata de um paraboloide, podemos usar coordenadas cilíndricas:
Para descobrir os limites vamos usar as equações dadas pelo enunciado:
O outro dado que podemos tirar do enunciado é
Como não há outro tipo de restrição
Passo 4
Voltando pra integral
Fazendo uma substituição simples:
Voltando pra integral:
Passo 5
Agora vamos calcular
Lembrando que a superfície é o disco de raio 1, centrado na origem e no plano .
Vamos começar parametrizando a superfície. Como se trata de um disco, podemos usar coordenadas polares
Passo 6
Hmm, aqui pode ter uma confusão galera, tomem bastante cuidado! O enunciado diz que a normal do paraboloide tem componente negativa, ou seja, aponta para fora do sólido.
Quando passamos para o disco , temos que manter a forma como pensamos na hora de montar o teorema: A normal deve apontar para fora do sólido.
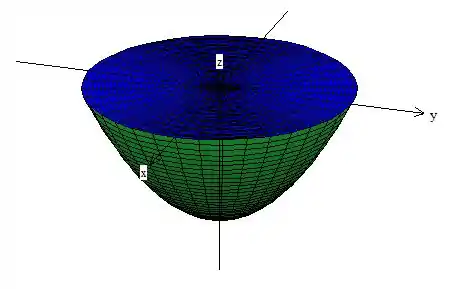
Voltando pro nosso esboço, a normal do disco tem que apontar para cima nesse caso aqui! Só assim que vai estar para fora do sólido, então a componente é positiva mesmo, tranquilo?