Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Superfície Aberta

Ver Teoria
Exercício 1412345678910111213151617181920212223242526272829303132333435363738394041424344454647

Enunciado

18) Seja f : R 3 → R de classe C 2 , tal que ∇ 2 f = x 2 + y 2 e

∂ f ∂ z x ,   y ,   1 = 1 3

Para todo x ,   y ,   1 ∈ R 3 .

Calcule

∬ S   ∂ f ∂ n →   d S

Onde S é a lata cilíndrica com fundo e sem tampa dada por x 2 + y 2 = 1 , 0 ≤ z ≤ 1 , z = 0 , com vetor normal n → apontando para fora de S .

Passo 1

Pow, para começar o nosso problema bem vamos entender o que o problema quer da gente, ok?

Ele nos pediu para que calculemos...

∬ S   ∂ f ∂ n →   d S

Mas que integral de superfície é essa? Bem, se você se lembrar que uma derivada direcional de uma função f é na realidade...

∂ f ∂ n → = ∇ f ⋅ n →

Na integral de superfície...

∬ S   ∂ f ∂ n → d S = ��� S   ∇ f ⋅ n →   d S

HUMMM! Veja que interessante esse dado! Se chamarmos o gradiente de um campo de vetores de F →

∇ f = F →

Então...

∬ S   ∇ f ⋅ n →   d S = ∬ S   F → ⋅ n →   d S

Veja que isso pode ser feito perfeitamente, afinal o gradiente é um vetor e F → também.

Ótimo, então o que o problema quer na realidade então é uma integral de superfície onde o campo F → é um campo especial: é um campo gradiente de uma função f qualquer 😉!

Passo 2

Humm! O problema não nos deu muitas informações sobre a função f então não vai dar para calcular essa integral de superfície de uma forma direta, por isso vamos pensar em uma outra forma de resolver integrais de superfícies: o Teorema de Gauss:

∬ ∂ W   F → ⋅ n →   d S = ∭ W   d i v   F →   d V

Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:

1º - Uma superfície fechada ∂ W delimitando o sólido W .

2º - Sem singularidades na função Vetorial.

3º - Superfície orientada positivamente.

Vamos passar por cada um deles e verificar se satisfazem ou não 😊!

Passo 3

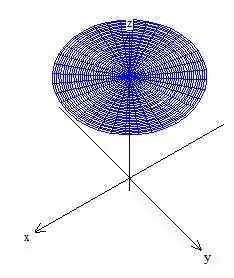
Quanto ao primeiro quesito, ter uma superfície fechada, já falhamos. Afinal de contas a nossa lata é uma superfície aberta na parte de cima em z = 1 :

Ora! Se a lata só não é fechada por um círculosinho em cima do plano z = 0 , fechamos esse cara com essa tampa!

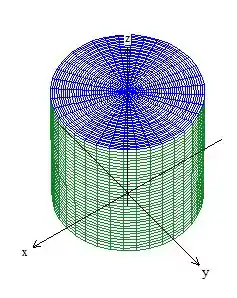
A essa superfície que acabamos de adicionar, daremos um nome de S 2 , mas não se preocupe, é apenas um nome ok?

Passo 4

Quanto ao segundo e ao terceiro quesitos...

2º - Sem singularidades na função Vetorial:

Está sendo satisfeito, pois o problema disse que o campo a função f era de classe C 2 , saca? Então de fato o gradiente de f existe 😉 e vale a função vetorial que estamos chamando de F → !

F → = ∇ f

3º - Superfície orientada positivamente:

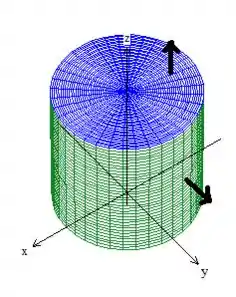
Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado:

“ n → apontando para fora”

Passo 5

Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...

∬ ∂ W   F → ⋅ d S → = ∭ W   d i v   F →   d V

Aqui só tenho um detalhe que preciso te falar! A integral de superfície do teorema é calculada em cima da superfície que fecha o sólido W . E esse cara é

∂ W = S ∪ S 2

Logo, temos que desmembrar a integral de superfície em duas... ∬ S   F → ⋅ n →   d S + ∬ S 2   F → ⋅ n →   d S = ∭ W   d i v   F →   d V

Vamos só fazer mais simplificações aqui... Passando a integral de S 2 pro outro lado...

∬ S   F → ⋅ n →   d S = ∭ W   d i v   F →   d V - ∬ S 2   F → ⋅ n →   d S

Passo 6

Eu sei que parece loucura trocar o cálculo de uma integral de superfície por outras duas integrais! Mas pode acreditar talvez é o único jeito mesmo ainda mais nesse caso 😐!

Mas vamos começar aqui então pela integral tripla...

∭ W   d i v   F →   d V

Bem, esse divergente aí tem uma outra notação sabia? Essa outra notação vai nos ajudar:

d i v F → = ∇ ⋅ F →

O seja, é o produto escalar entre o operador de derivadas parciais pelo campo F → ... Como F → vimos que definimos como ∇ f

∇ ⋅ F → = ∇ ⋅ ∇ f =

∇ 2 f

Então a integral tripla fica sendo...

∭ W   d i v   F →   d V = ∭ W   ∇ 2 f   d V

Esse cara para a alegria de geral, foi dado ;D

∇ 2 f = x 2 + y 2

∭ W   ∇ 2 f   d V = ∭ W   x 2 + y 2   d V

Passo 7

Essa integral se mata fazendo uma mudança para coordenadas cilíndricas...

x = r cos ⁡ θ

y = r sin ⁡ θ

z = z

J = r

Onde o r no cilindro varia de 0 até o raio máximo que é o raio do cilindro 1 :

0 ≤ r ≤ 1

Quanto ao θ , bem vemos que na lata ele precisa de dar uma volta completa...

0 ≤ θ ≤ 2 π

Quanto a variação de z , basta ver que o cilindro varia de 0 até a altura máxima que é 1 ...

0 ≤ z ≤ 1

Passo 8

Logo...

∭ W   x 2 + y 2   d V = ∫ 0 2 π ∫ 0 1 ∫ 0 1 r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ ⋅ J   d z d r d θ =

∫ 0 2 π ∫ 0 1 ∫ 0 1 r 2 cos 2 ⁡ θ + sin 2 ⁡ θ ⋅ r   d z d r d θ = ∫ 0 2 π ∫ 0 1 ∫ 0 1 r 3   d z d r d θ

Integrando em z ...

∫ 0 2 π ∫ 0 1 ∫ 0 1 r 3   d z d r d θ = ∫ 0 2 π ∫ 0 1 r 3 ∫ 0 1 1 d z   d r d θ =

∫ 0 2 π ∫ 0 1 r 3   d r d θ =

∫ 0 2 π r 4 4 0 1 d θ = 1 4 2 π =

1 2 π

Passo 9

Concluímos uma etapa, mas ainda nos falta encontrar qual é o resultado da integral de superfície de F → em cima de superfície que adicionamos, ou seja, a tampa onde z = 1 ...

∬ S 2   F → ⋅ n →   d S

Bem, a única informação que temos nesse plano z = 1 é que...

∂ f ∂ z x ,   y ,   1 = 1 3

Bem, voltando como F → = ∇ f , então a integral de superfície fica...

∬ S 2   F → ⋅ n →   d S = ∬ S 2   ∇ f ⋅ n →   d S

O vetor n → por ser um vetor normal unitário apontado pra cima...

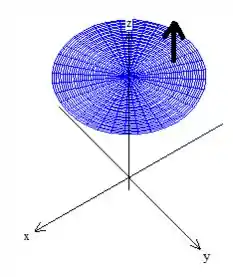
Pode ser escrito como...

0 ,   0 ,   1

O gradiente de f em cima de z = 1 é dado por...

∂ f ∂ x x ,   y ,   1 ,   ∂ f ∂ y x ,   y ,   1 ,   ∂ f ∂ z x ,   y ,   1

Logo...

∬ S 2   ∇ f ⋅ n →   d S = ∬ S 2   ∂ f ∂ x x ,   y ,   1 ,   ∂ f ∂ y x ,   y ,   1 ,   ∂ f ∂ z x ,   y ,   1 ⋅ 0 ,   0 ,   1   d S =

Resolvendo esse produto escalar...

∬ S 2   ∂ f ∂ z x ,   y ,   1   d S = ∬ S 2   1 3   d S

Veja que legal! Saímos de um cara que não sabíamos e caímos numa coisa bem mais conhecida:

∬ S 2   1 3   d S = 1 3 ∬ S 2     d S

O que é a integral de 1 d S ? Yes! É a área da superfície S 2 que é uma circunferência de raio 1 ...

1 3 π 1 2 = π 3

Passo 10

Bem, pelo teorema de Gauss, então conseguimos a integral de superfície em cima da lata que é a integral tripla mais a integral em cima da tampa:

∬ S   F → ⋅ n →   d S = ∭ W   d i v   F →   d V - ∬ S 2   F → ⋅ n →   d S

∬ S   F → ⋅ n →   d S = π 2 - π 3 =

π 6

Resposta

π 6