2) Calcule
onde e com e
Passo 1
Felizmente sabemos que existem dois métodos de resolução de integrais de superfície:
1º - Método direto.
2º - Teorema de Gauss.
O método direto no nosso caso daria certo trabalho, já que tem um no campo vetorial. Por isso a ideia é já ir pensando no Teorema de Gauss. Para ter uma noção mais clara se esse teorema vai ajudar ou não, calculemos o divergente...
Como...
Sim, um divergente, bem fácil sugerindo ainda mais que apliquemos esse método.
Passo 2
O teorema nos diz:
Mas antes de aplicar a igualdade, devemos averiguar certas condições:
1º - Um sólido sendo delimitado pela superfície borda .
2º - Um campo sem singularidades onde estamos trabalhando.
3º - Uma orientação superfície sólido positiva.
Passo 3
A primeira condição, a de ter um sólido sendo delimitada por uma superfície fechada borda, caso desenhamos um esboço da superfície, vamos perceber que ela não satisfaz, afinal é um paraboloide passando por e sendo delimitado por ...
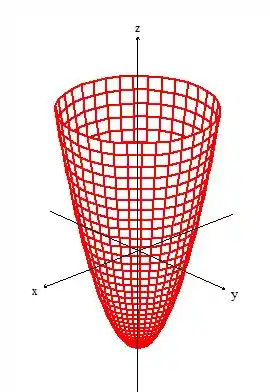
Mas repare que podemos fechar esse cara com a tampa , ...
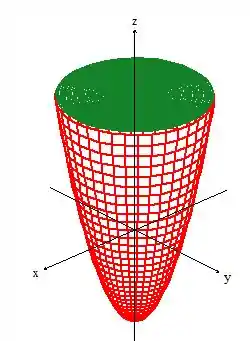
Pow, o sólido agora se definiu dentro desse cara. A borda dele é justamente a união da superfície com a que acabamos de adicionar... . Assim, a igualdade fica...
Passo 4
Precisamos de um campo sem singularidades... O que já acontece há um tempo, afinal
O campo não tem singularidades como uma divisão por um ponto nulo ou outra coisa bizarra assim, sacou?
Passo 5
Finalmente, a última condição, mas não menos importante, trata-se da questão de orientação. Precisamos de um campo de vetores normais saindo do sólido.
Felizmente é o que o problema quer, afinal...
Isso significa que o vetor normal está apontando, em cima da superfície , para onde a coordenada é negativa, ou seja, para baixo...
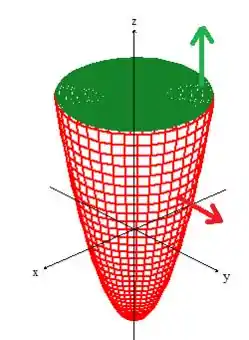
Basta colocarmos o vetor na superfície que adicionamos, a , pra cima e prontinho ;)
Passo 6
Já podemos aplicar o teorema...
Se queremos a integral de superfície em cima de , basta isolar...
E calcular essas duas integrais que surgiram. Bora?
Passo 7
Começando pela integral de tripla...
Repare que o sólido, por estar dentro de um paraboloide, pode ser descrito em coordenadas cilindricas:
Onde o e o , variam na projeção do sólido no plano , como se olhássemos de cima para baixo:
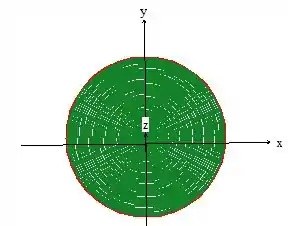
Repare que o , varia de até o limite máximo, dado pela intersecção do plano com a equação do paraboloide...
Portanto um cilindro de raio ...
Enquanto o varia...
O , varia do paraboloide até o plano ...
Passo 8
Com essas variações...
Podemos retornar a integral tripla...
Calculando a integral...
Como ...
Passo 9
Calma que ainda nos resta calcular a integral e superfície em que adicionamos ao problema...
Se parametrizarmos essa superfície ...
O vetor normal unitário a esse pedacinho de plano é ...
Como
A integral de superfície de é a área da superfície. Como é um circulo de raio igual a ...
Passo 10
Voltando para o teorema de Gauss que adaptamos...
Passo 11
Resposta
Ei, a resposta está no passo a passo :)