21) Calcule
Sendo , através de , orientada de forma que o vetor normal no ponto seja o vetor .
Passo 1
O fluxo de um rotacional de um campo através de uma superfície é dado por uma integral de superfície
Como a superfície nos parece muito esquisita (uma paraboloide que a gente já já vamos ver), já é um indício de que iremos ter que utilizar o Teorema de Stokes, pois esse teorema relaciona
Passo 2
Mas não podemos aplicar essa igualdade assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:
1º - Uma curva fechada delimitando a superfície .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Passo 3
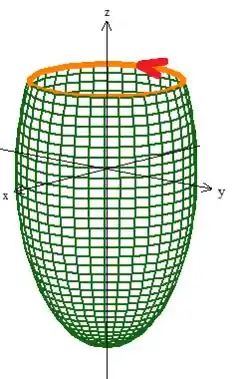
Para saber se o primeiro quesito é cumprido ou não, desenhemos a superfície : sabemos que é o elipsoide
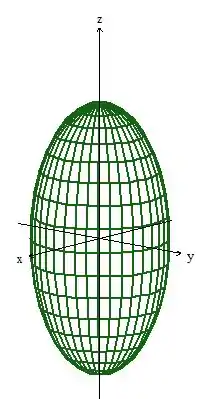
Mas cortado pelo plano ...
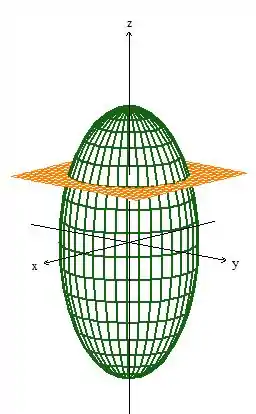
E eis que aparece o ali em baixo já que ...
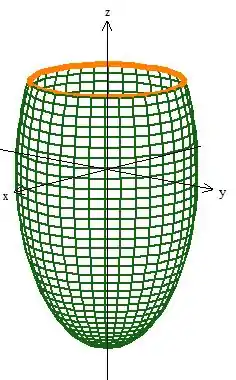
Veja então que a curva fronteira de é aquela circunferência ali, e ela é obtida na intercessão do plano com o elipsoide:
No caso é uma circunferência de raio ;D
Passo 4
Outra coisa que temos que averiguar é a condição do conjunto borda\superfície estarem orientados positivamente:
se você perceber essa a superfície está orientada de tal forma que o vetor normal lá em baixo no ponto o vetor normal está apontando para baixo, afinal ...
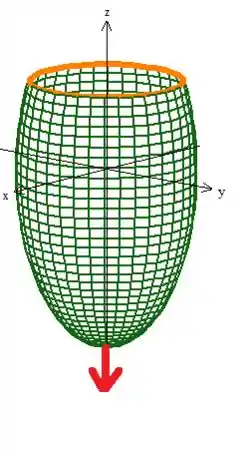
Então pela regra da mão direita, a borda deve estar girando no sentido horário:
E prontinho, agora elas estão orientadas positivamente 😉
Passo 5
A última exigência diz respeito a função vetorial
Precisamos de um campo sem singularidades! O que já acontece neh? Já que não temos nenhum bug no campo como pontos de divisão por ou algo assim 😊!
Passo 6
Com as condições de Stokes estando satisfeitas, podemos aplicar a igualdade linda entre as integrais:
Se queremos a integral de superfície, calculemos a integral de linha e está numa boa! Para isso vamos precisar seguir algumas coisineas:
1º - Parametrizar a curva
2º - encontrar o termo
3º - Substituir em os caras determinados na parametrização
Passo 7
Primeiro em relação a parametrização da curva : pametrizando com a parametrização polar...
Onde não é parâmetro, afinal como é uma curva só tem um parâmetro (). é o raio da circunferência que no caso ... Logo a parametrização final dessa borda é...
Onde tem que dar uma volta completa ao redor do , lodo...
Veja que infelizmente tem um erro na parametrização a cima 😐! A curva parametrizada dessa forma ela gira sempre no sentido horário saindo do eixo :
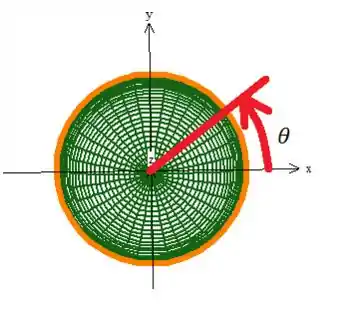
Porém... Queremos a curva girando no sentido contrário a esse sentido, ou seja, no sentido anti-horário!
Se invertermos os termos da parametrização dessa forma...
Agora a curva gira no sentido positivo, ou seja, no sentido horário como manda o vetor normal:
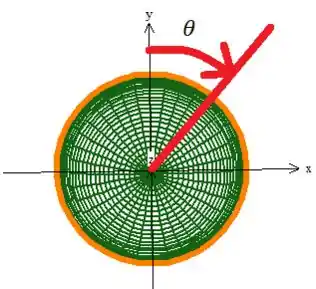
Então eia a parametrização final:
Passo 8
A curva já está parametrizada positivamente. Para o termo , basta derivar em relação a ...
O campo tem que ser transformado nas novas coordenadas (basta observar a parametrização) ...
Voltando para a integral de linha...
Calculando o produto escalar:
Agora é só resolver essa integral e correr para o abraço.
Passo 9
Lembrando que ...
Logo, pelo teorema de Stokes o fluxo do rotacional em ...